Mathematical Modeling of Cell Adhesion and Arterial Blood Flow

Understanding the adhesion and rolling of a white blood cell on the endothelium wall and its impact on the whole cardiovascular system flow and the blood flow through the aorta and its bifurcations motivate this dissertation.  Blood dynamics involves length scales across vastly different ranges.  An example is provided by leukocyte adhesion to a substrate, which is an important biomedical problem that has been the subject of extensive research.  Analyzing the adhesive and rheological behavior of leukocytes is essential not only for describing microcirculatory flow dynamics, but also for understanding cell function and behavior in health and disease.  Computational fluid dynamics (CFD) techniques provide us with powerful tools for tackling a variety of problems in engineering involving fluid flow accompanied by mass, momentum and energy transport. 

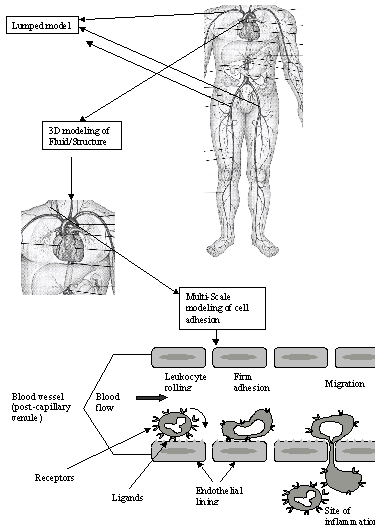
These methods have recently been applied to a variety of problems related to hemodynamics, such as cardiovascular and capillary fluid flow, cellular physics, and adhesion dynamics.

Issues spanning from cell surface receptors to blood flow in arteries involve disparate scales, as shown in the Figure.  A direct computation encompassing all relevant scales, from large vessels to receptor-ligand interaction is beyond the reach of current and foreseeable computational resources.  The multi-scale technique allows us to assess the effect of a reflected wave on the distribution of the flow through the aorta for example.  An effective overall model can be devised globally using the lumped (1D) model to estimate the pressure and flow rate at a given location, and locally, using the 3D field equations to analyze the detailed fluid flow in a given artery.

N'Dri, Narcisse.  Multi-scale computation in hemodynamics 2002.