Center of Gravity
The previous section noted the mobile platform is the key to your robot’s maneuverability. We will now expand on that statement and investigate the critical effects center of gravity (or CG) have on your robot’s stability.
The center of gravity is the average location of the weight of an object. Stated another way, the CG is the virtual balance point about which an object would perfectly balance if a string was attached at that exact location, as shown in figure 1 below. For the purpose of this course, each object can act as if all its weight is concentrated at a point mass located at the CG.
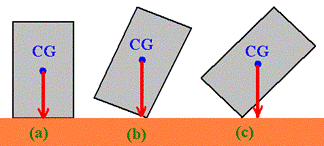
Figure 1: Example of object CG.
Because robots are comprised of many objects, it’s necessary to understand how to calculate (or for the purpose of this course, at least estimate) the combined (or composite) CG location for an assembly of parts. Assuming the individual pieces each have a CG at their geometric centers, the CG calculation involves equating the moment produced by the composite CG location with the summation of the moments produced by each individual piece. As learned in statics, the exact point about which the moments are summed is not important, so we will arbitrarily choose point 0 in figure 2.
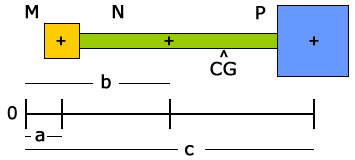
Figure 2: Calculating combined CG of multiple objects.
Since the requirement for static equilibrium is that the summation of the moments acting about any point must be zero, we can easily write the governing equation as:
CG × (WM+WN+WP) = a × WM +
b × WN + c ×WP
Where WM, WN, WP are the weights of each object, a, b, c, are the distances from each object’s CG to the point about which the moments are being calculated, and CG is the computed distance to the combined structures’ composite CG.
The important takeaway from this exercise is to look at figure 2 and develop a practical understanding about CG computation for composite assemblies. In simple terms, you can see since the weight of object P is much larger than that of object M, the combined CG location is shifted towards the heavier object. It should also be obvious if WM and WP were equal, the composite CG location of the assembly would be exactly in the center of object N. This understanding is important for the next section.
Effects of CG Location on Traction:
As discussed previously, one of the principal benefits of 3-wheel mobile platforms is that each drive wheel always remains in contact with the driving surface. When that is the case, the amount of traction available to each drive wheel is proportional to the amount of force (i.e. weight) on each drive wheel. Therefore, when in the design phase, earnestly try to position heavier items closer to the drive wheels, as illustrated in figure 3 below. Notice how much closer the composite CG location is to the large drive wheels in the left pair of sketches compared to the right pair.
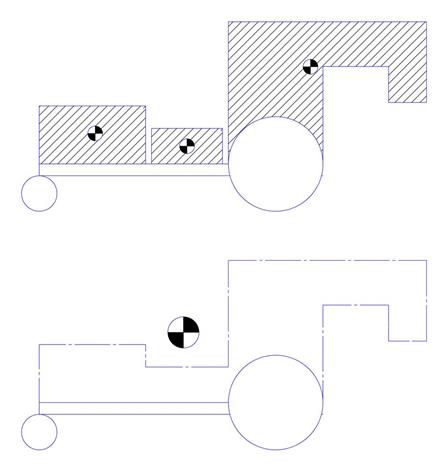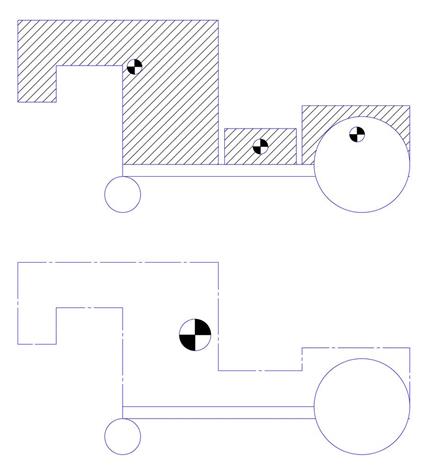
Figure 3: Components placed with (LEFT) and without (RIGHT) regard for composite CG’s impact on robot traction.
If it is not possible to achieve a favorable CG location by changing component positions with a design concept, consider using ballast to shift the composite CG closer to the drive wheels, as shown in figure 4 below.
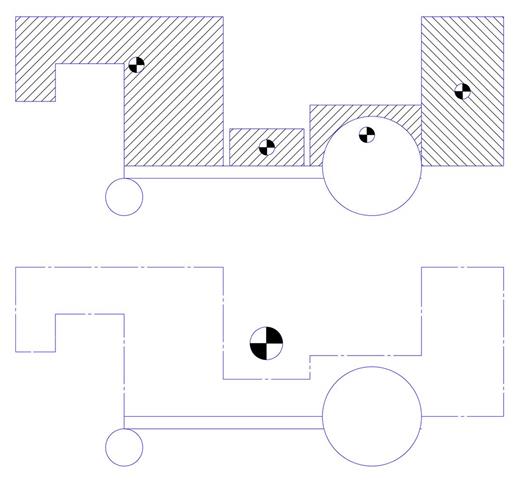
Figure 4: Ballast (extra weight) added to shift the composite CG location closer to the drive wheels for increased traction.
Ballast is the term for additional weight added for the sole purpose of shifting the composite CG location to a more favorable position. Notice how the ballast shown in figure 4 shifts the composite CG location of the design shown in figure 3(b) towards the robot’s drive wheels, thereby increasing traction and controllability. The downside to using ballast is that you are adding more overall weight to the robot, which in turn requires more torque output from the mobile platform’s drive wheel motors.
Effects of CG Location on Stability (i.e. Tipping):
Composite CG location also has a large effect on robot stability, or specifically, its resistance to tipping. As illustrated in figure 5, the higher the CG position, or the closer it is to one of robot’s roll axes, the greater the propensity of the robot to tip over due to dynamic acceleration forces. If we sum the tipping moments about the point of contact between the drive wheels and the ground we get:
Fh × h1 = Fv × l1
Where Fh is the inertial force due to acceleration in the horizontal direction, h1 is the distance to the ground, Fv is the acceleration in the vertical direction due to gravity, and l1 is the distance to the contact point. Since gravity is a constant, there are three ways to maximize robot stability against tipping: (1) reduce the CG height, (2) maximize the distance between the CG and the roll axes, (3) increase the mass of the robot.
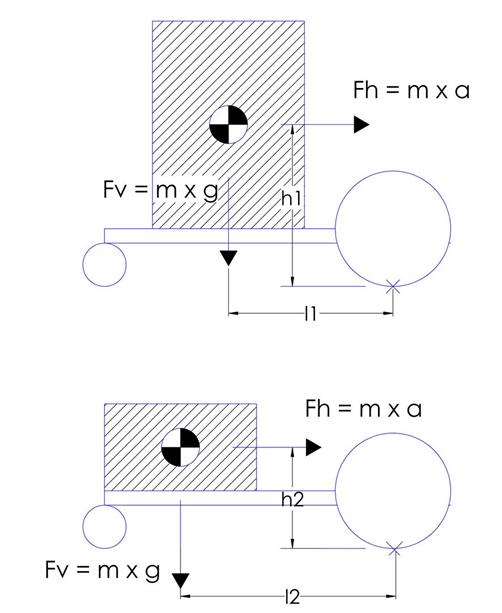
Figure 5: Acceleration / inertial forces responsible for robot stability in the
longitudinal (forward/backward) direction.
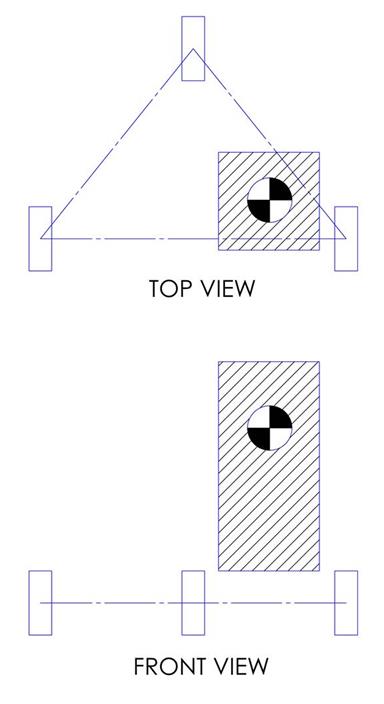
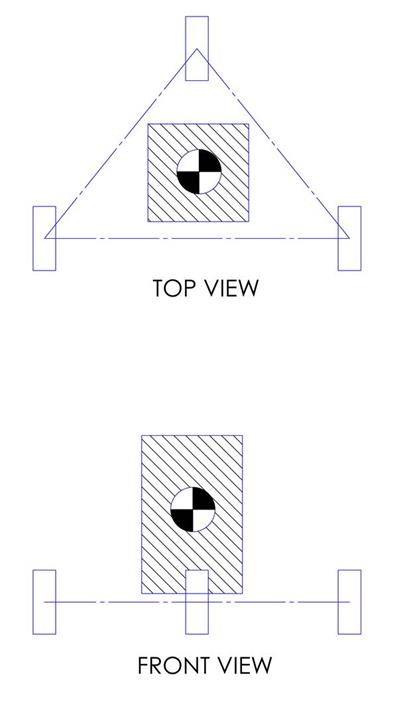
The final consideration is in regards to stability in the lateral (or side-ways) direction. As shown in figure 6 below, the same advice presented above in the longitudinal direction applies in the lateral direction: try to minimize the composite CG height and maximize the distance between the CG location and any of the robot’s roll axes.
Figure 6: Comparison of poor CG location (too close to a roll axis and too high) (LEFT) versus much improved CG location (centered between roll axes and low) (RIGHT).