
Volterra Kernels to Model Nonlinear Aeroelasticity
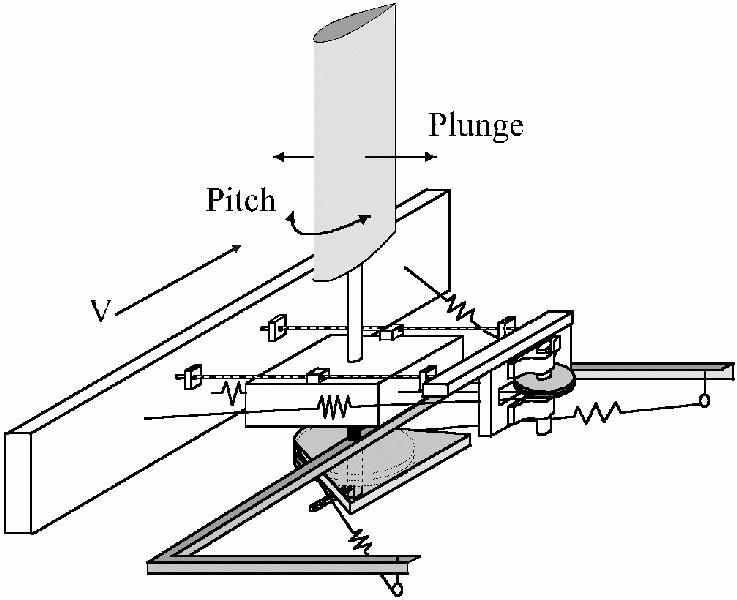
1. Introduction| The initial work for this project has been considering a testbed constructed at Texas A&M University under the direction of Professor Thomas Strganac. This testbed, as shown in the photo on the right, is a wing section mounted in a wind tunnel. The section is allowed to move in both pitch and plunge directions. As such, the dynamics of this system are similar in nature to the traditional bending-torsion dynamics associated with aeroelastic flight vehicles. | 
|
| Nonlinearities are introduced to the dynamics by altering springs and cams on the system. The isometric drawing of the testbed, shown at right, indicates several mechanisms that may be altered. The nonlinearity that will be considered for this study is a nonlinear spring stiffness. Specifically, a hardening spring is included with the pitch degree of freedom. This spring is represented by a 5th-order polynomial and is valid for pitch angles up to 20 deg. |
|
| The estimation of the nonlinearity actually uses responses from both the nonlinear dynamics and the linear model. These responses are shown in the figure on the right. Clearly the responses from the linear model and nonlinear system are different. One notable difference is the bias associated with the nonlinear system because of the asymmetric spring stiffness. Another notable difference is the magnitude variations between the linear model and nonlinear system caused by the hardening spring. | 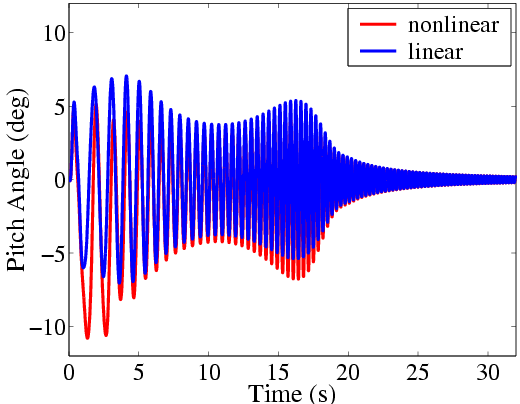
|
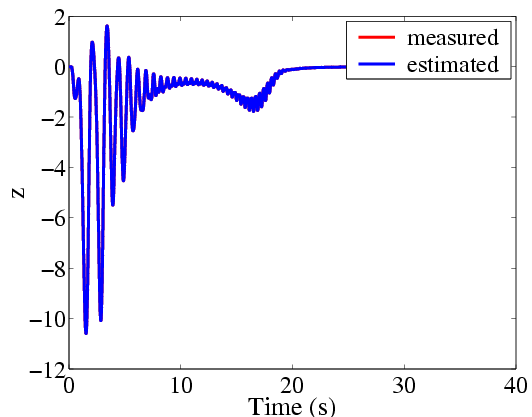
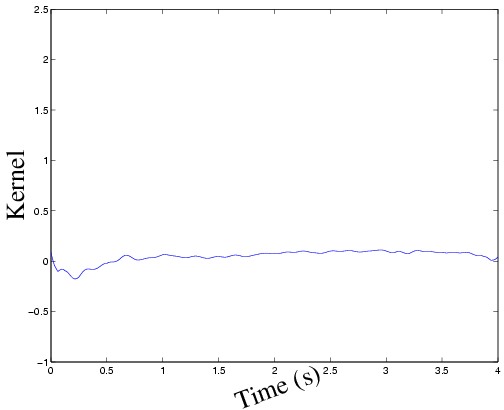
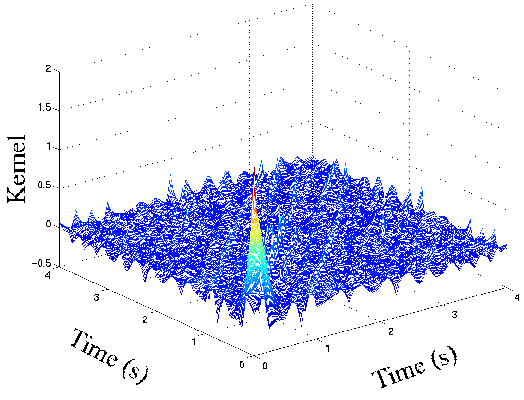
| Volterra kernels are computed to represent a mapping between the signal, z, and the pitch angle. The first-order and second-order kernels are presented in the figures below. The figure on the left shows the first-order kernel is quite small while the figure on the right shows the second-order has a large narrow peak. These results are expected because the kernels are associated with data that is purely nonlinear. |
 |
 |