

EGM4313
INTERMEDIATE
ENGINEERING ANALYSIS

Instructor-U.H.Kurzweg
|
"The winds and
waves are always on the side of the ablest navigator"-Edward
Gibbon (1737-1794)
"Eternity is really long, especially near the
end"-Woody Allen (1935- )

This is one of several WEB pages which I have
constructed over the past decade for courses in mechanics and
applied mathematics here at the University of Florida . The
present page is intended as a suplement the the four credit
course EGM 3413
dealing with the topics of vector fields, solution of ODEs by
matrix methods, partial differential equations, and functions
of a complex variable.
The fractal shown above is generated by a MATLAB program
using the iteration Z[n+1]=Z[n]^6 - 1.12 . It's amazing that
such a simple iteration will generate such an intricate
six-fold symmetric figure.
The book we
are using is Advanced
Engineering Mathematics by E. Kreyszig 8th Ed. John
Wiley&Sons, Inc. The book has a few flaws such as using Ao
instead of Ao/2 in the standard Fourier series, using c^2
instead of alpha as the thermal diffusivity, and giving a poor
discusion of the characteristic variables in PDEs, but then it
is still the best of the comprehensive intermediate
engineering math texts available. An OUTLINE for the course is found by clicking HERE.You will find this material
to be an essential part of the modern engineer's repertoire.
You can reach me anytime at e-mail
kurzweg@ufl.edu .
Your
course grade will based on three hour exams(30% each) plus
weekly homeworks (10% total). There will be no final exam. To see the topics of this week's lectures
scroll down the page until you encounter the knight on
horeseback. Click on the
underlined stuff below to obtain additional information on the
topics being discussed.

Here is a little cartoon to start things off-

<>
FIRST WEEK:
 Today will be our first
lecture in EGM 4313. We will devote the time to a review of
vectors, talking about dot and cross products , the scalar and
vector triple. What we mean by scalar and vector fields, and
introduce the directional derivative and the gradient. (Chapter 8)
Today will be our first
lecture in EGM 4313. We will devote the time to a review of
vectors, talking about dot and cross products , the scalar and
vector triple. What we mean by scalar and vector fields, and
introduce the directional derivative and the gradient. (Chapter 8)
HERON'S
FORMULA: A famous formula due to
Heron of Alexandria is that for the area of any triangle when
the length of its three sides are given. This formula
states that the square of the area of any triangle is given by A^2=s(s-a)(s-b)(s-c), where a, b and c
are the lengths of the sides of the triangle and s= (a+b+c)/2 is the half-perimeter. I
first ran into this formula during my high school geometry class
and remember asking my teacher how this formula is derived. He
did not know and I found out later that the geometric proof,
first given by Heron * in about
100AD, is quite complicated and based on inscribing a circle in
a triangle. I'll give you here a quick reverse proof using
algebra and vector concepts we have talked about in the first
lecture. Assume the formula is correct and rewrite it as A^2=[(a+b)^2-c^2][c^2-(a-b)^2]/16 . Now
place the three corners of your triangle at A with coordinates
(0,0), at B with coordinates (bx,by) and at C with coordinates
(cx,0). The corresponding side lengths are then
a=sqrt[(bx-cx)^2+by^2], b=cx, and c=sqrt[bx^2+by^2].
Substituting these quantities into the above A^2 formula, we
find after a bit of manipulation that things reduce to the very
simple form A=[by][cx]/2 , which
is the known area of the triangle via vector calculus when
taking half of the absolute value of the cross product between
the triangle edge vectors ibx+jby and icx. This vector product
result is much simpler than (but equivalent to) the Heron
formula and can be used to calculate the area of any polygon by
simply adding up the areas of the triangles making up the
polygon. Such formulas are often used for determining the
acreage of land within a polygonal boundary. For a right
triangle one has , via the Pythagorean Theorem**, that a^2+b^2=c^2 and hence that the
triangle area becomes A=a*b/2.
*-Heron of
Alexandria(65-125AD) was an expert in geometry and mechanics
working at the greek school in Alexandria, Egypt . In addition
to the Heron formula, he is also known for the invention of
the aeolipile, a steam filled hollow sphere which rotates
about a fixed axis by the action of steam jets. He can thus
also be considered the grandfather of the steam turbine and
the jet engine.
**-Pythagoras was born in 569BC on the island
of Samos, Greece and is considered by many the first pure
mathematician . He developed mathematical concepts
including a proof for the Pythagoran Theorem. The actual
result that a^2+b^2=c^2 for a right triangle was already
known earlier(about 1900BC) by the Babylonians and
Pythagoras may have become aware of it during his travels to
Syria and Egypt. Click HEREto
see the best kown ancient proof of the Pythagorian Theorem
given by Euclid(325-265BC) in his book Elements. A
simple extention of a geometrical Pythagorean Theorem proof
can be used to derive the familiar Law of Cosines shown HERE.
LAWS FOR TRIANGLES: In much of our subsequent discussions
it will be assumed that the students are thoroughly familiar with
the basic laws for oblique triangles. Go HERE to review
these.
DIRECTIONAL DERIVATIVE AND
THE GRADIENT- Consider a function
f(x,y,z)=C defining a collection of surfaces in 3D space. The
directional derivative of f(x,y,z) is defined as df/ds, where
ds indicates the direction in which the derivative is taken in
the 3D space. A simple chain rule manipulation shows df/ds=(df/dn)*(dn/ds)=grad(f). t , where
t is the unit vector along ds and n is the unit
surface normal to the surface f=C. The new vector , called
the gradient of f or simply grad(f), can be written in
cartesian coordinates as grad(f)=ifx+jfy+kfz , with the
subscripts indicating partial derivatives. Note that when ds is in the direction normal
to the surface f=C , then the directional derivative will have
its maximum value of df/ds=abs[grad(f)]. Also when ds is in a
direction parallel to the surface f=C, then df/ds is
necessarily zero. Click HERE to view a picture of df/ds. You can also
click HERE to see a 2D temperature field T(x,y)(in blue)
and the corresponding heat flow direction corresponding to
grad[T(x,y)] (in red).
A SUPPLEMENTAL SOURCE FOR
VECTOR CALCULUS DEFINITIONS-There
are numerous links on vectors and vector fields found on the
WEB. Here is one you might want to look at-
http://www-solar.mcs.st-and.ac.uk/~alan/MT3601/Fundamentals/Fundamentals.html
TANGENT PLANE TO A SURFACE: In class today we defined the gradient to a
surface and showed how a tangent plane to the surface has its
normal point in the same direction as the gradient. I give HEREanother example of such a calculation for a
point xo,yo,zo on a paraboloid z=1-x^2-y^2. A plane tangent to
this surface is given by a(x-xo)+b(y-yo)+c(z-zo)=0, where an b
and c are constants to be found. Now the gradient of the
paraboloid is grad(u)=2xoi+2yoj+k and the normal to the plane
is n=ai+bj+ck. Since the vectors n and grad(u) must be
parallel, we conclude that a=2xo, b=2yo, and c=1. Hence the
tangent plane becomes 2xo(x-xo)+2yo(y-yo)+(z-zo)=0.
 More on the gradient and the directional
derivative. Length of a Space Curve. Also concept of the
divergence of a vector and the curl of a vector. Some vector identities involving these three
operations.
More on the gradient and the directional
derivative. Length of a Space Curve. Also concept of the
divergence of a vector and the curl of a vector. Some vector identities involving these three
operations.
DIVERGENCE OF A VECTOR
FIELD: A second important
operation in vector analysis is the divergence of a vector
field V. The simplest way to envision the divergence of
V(x,y,z) is to think of V as the velocity field for a fluid
flow passing through an incremental cube as shown HERE. The net outflow of fluid through this volume
divided by the volume then represents the divergence of
this vector flow field V and is designated as div(V). Note
that div(V) is a scalar quantity while V is a vector quantity.
CURL OF A VECTOR FIELD: This is the third important vector
manipulation in vector calculus and is equal to the
circulation of a vector field V about a closed curve
divided by the area within the curve. Mathematically one has curl(V)=det[i, j, k; d/dx, d/dy, d/dz; u, v,
w] , which is a new vector field.
For example curl(iy-jx)=det[i, j, k; d/dx, d/dy, d/dz; y, -x,
0]= -2k. Note that the curl[grad(F)] is always zero as is
div(curl(V)).
SECOND WEEK:
 Expression of grad,div and curl in other
orthogonal coordinate systems.Vector manipulations used
to formulate equations of electromagnetic wave propagation, heat
flow, and 2D incompressible and inviscid fluid flow behaviour.
Line integrals and independence of path.
(End of Chapter 8 and beginning of Chapter 9)
Expression of grad,div and curl in other
orthogonal coordinate systems.Vector manipulations used
to formulate equations of electromagnetic wave propagation, heat
flow, and 2D incompressible and inviscid fluid flow behaviour.
Line integrals and independence of path.
(End of Chapter 8 and beginning of Chapter 9)
INTEGRATION OF SURFACE AND
VOLUME INTEGRALS USING ORTHOGONAL COORDINATE SYSTEMS: I have noticed from some of the questions you
have been asking me, that many of you have difficulty in
evaluating multiple integrals in coordinate systems other than
cartesian. The procedure is really very much straight forward.
If you take any orthogonal system u,v,w, then a volume
increment there is dV= huhvhw
dudvdw and a surface increment is dS=huhvdudv,
where hu, h v and hw are the
scale factors. These scale factors depend on the particular
orthogonal coordinate system being used and can be determined
by the invariance of an increment of length squared ds^2 in
space. For a cylindrical system we have (h r, htheta
, hz )=(1, r, 1) while for a spherical system one
has(1, r, r*sin(theta)). Consider now the volume of a sphere
of radius r=a. It is given by
Integral[dV]=Integral[r^2*sin(theta)*dr*d(theta)*d(phi)], when
expressed in spherical coordinates. The range of integration
is 0< r<a, 0<theta<Pi for the polar angle theta,
and 0<phi<2*Pi for the azimuthal angle phi. This very
simple triple integration yields V=(4/3)*Pi*a^3 and is a much
easier integration than if done in a cartesian system(x,y,z).
Consider next the total surface area S of a cylinder of radius
b and height H. Here one has (choosing cylindrical coordinates
) that S==2*Pi*b^2+Integral[r*d(theta)*dz], with range
0<theta<2*Pi , 0<z<H and r=b. Thus S=
2*Pi*[r^2+b*H]. It is also easy to show that the cylinder
volume is V=Pi*b^2*H . The famous mathematician Archimedes * first showed
that the ratio of the volume of the largest sphere of radius b
which can be put into a cylinder of the same radius and of
height H=2b is[(4/3)*Pi*b^3]/[2b*Pi*b^2]=2/3. He was so proud
of this result that he had a picture of a sphere in a cylinder
engraved on his tombstone.
Note that the scale
factor triple product huhvhw is
equivalent to the absolute value of the Jacobian of the
transformation equations relating the cartesian system
(x,y,z) to the particular orthogonal system(u,v,w) of
interest. A good discussion of scale factors and vector
operations in various orthogonal coordinate systems
(including cylindrical, spherical, elliptic, parabolic,
toroidal, and bipolar) can be found in the book"Mathematical
Methods for Physicists" by G. Arfken(3rd ed. Academic Press
1985).
* Archimedes of
Syracuse(287BC-212BC)-Greatest mathematician and mechanical
genius of ancient times. Born and died in Sicily but spent a
good part of his time at the greek school(library) in
Alexandria, Egypt. He discovered the Archimedes
Principle
of Buoyancy , showed that Pi =3.14159...has a value
less than 3+1/7 but greater than 3+10/71, invented the Archimedes
screw for pumping water, and developed defense
machines including a solar concentrator for burning the
sails of ships. He was killed by a Roman soldier during the
Second Punic War. On a recent(2005) visit to Syracuse
in Sicily, I asked our tour guide about the location of
Archimedes's grave. It seems nobody knows although there are
three to four sites throughout the city which claim that
distinction. Sounds to me a lot like "Washigton Slept
Here"stories. Anyway HERE
is a picture of the Ear of Dionysus, an extant archeological
site in Syracuse dating to the time of Archimedes.
CURVE LENGTH USING THE
POSITION VECTOR: We can describe
a space curve in terms of its position vector
R(t)=ix(t)+jy(t)+kz(t). Taking the time derivative dR/dt one
gets a vector increment along the curve itself, so that the
curve length becomes L=Int[sqrt(R'(t).R'(t)),t=t1..t2]. this
last dot product term is equivalent to ds=sqrt(dx^2+dy^2+dz^2)
as you encountered earlier in calculus. Click HEREto see the method applied for determining the
length of the cardioid
curve r=(1-cos(t).
 Line Integrals
and Surface Integrals. Derivation and application of the
Divergence(Gauss)
Line Integrals
and Surface Integrals. Derivation and application of the
Divergence(Gauss)
Theorem , and the Stokes Theorem. (Chapter
9)
WHO WAS GAUSS? -Karl
Friedrich Gauss(1777-1855) was a mathematician and astronomer
who spent most of his professional life at the University of
Goettingen as director of their observatory. He is considered
the "Prince of Mathematicians" on a footing equal to Archimedes
and Newton. His works include investigations on the fundamental
theorem of algebra, the prime number theorem, the least squares
method, and non-Euclidian geometry. He also carried out geodesic
surveys, invented the heliotrope and calculated the orbit of the
asteroid Ceres. He showed how one can construct a regular
seventeen sided polygon (heptadecagon) using only a straight
edge and compass. Furthermore he showed that it is always
possible to construct a regular polygon this way as long as the
number of sides equals a Fermat Prime (ie. (2^2^n)
+1=3,17,257,etc ). The divergence theorem is named after him and
also the hypergeometric series . You can find out more about him
by going to Gauss.
An image of KFG wearing a cap and a rather dour expression is
found HERE.
WHO WAS GEORGE GREEN? George Green(1793-1841) was the son of a
baker in Sneinton, Nottingham, England . He was a
mathematical genius, although his formal education had
stopped with grade shool. His occupation was that of miller
and his hobby was mathematics, which he largely learned on
his own. In 1828 he wrote the first of his ten or so
remarkable scientific papers. This first paper, entitled "An
Essay on the Application of Mathematical Analysis to
Theories of Electricity and Magnetism" , brought him to the
attention of the scientific establishment and he was invited
and then began to attend Cambridge University as an
undergraduate at the ripe old age of forty. Unfortunately
his health deteriorated and he died a few years later at the
age of 48. His name is associated with Green's theorem and
the various Green's formulas and he is also credited with
invention of the Green's function. He was never married but
had seven children with the daughter of his mill foreman.
3RD WEEK: (more from Chapter 9)
 Green's
Theorem as a special case of Stokes Theorem. Green's Theorem
used to determine the areas bounded by various curves including
the cardiod. Also the derivation of Green's first and second
formulas from the divergence theorem. Evaluation of Surface
Integrals.Evaluation of some problems from
the book.
Green's
Theorem as a special case of Stokes Theorem. Green's Theorem
used to determine the areas bounded by various curves including
the cardiod. Also the derivation of Green's first and second
formulas from the divergence theorem. Evaluation of Surface
Integrals.Evaluation of some problems from
the book.
AREA DETERMINATION USING
GREEN'S THEOREM: In class last
time we derived Green's Theorem from the Stokes theorem and
showed that the area integral of the partial of Q(x,y) with
respect to x minus the partial of P(x,y) with respect to y is
equal to the line integral of Pdx+Qdy around the curve C
bounding the area. By setting Q=x and P=0 one finds that the
area for any simply connected region equals the line
integral of xdy about the bounding curve. If one uses polar
coordinates the area becomes 0.5*lineintegral[r^2 d(theta)].
To demonstrate this result we consider the area contained
within the Rhodonea curve r=cos(2*theta) . Doing the line integration using MAPLE we
find the following
EVALUATION OF A SURFACE
INTEGRAL USING THE DIVERGENCE THEOREM: Suppose that we wanted to find the surface
integral of x^2 taken over the hemisphere x^2+y^2+z^2=1,
z>0. One way to quickly do this is to consider the
divergence theorem for the vector field V=ix over this
hemisphere. Here the theorem says the hemisphere
volume, which is 2*Pi/3, just equals the surface integral of V
doted into the surface normal n. Across the bottom boundary of
the volume, where n=-k, there is no contribution since V.n=0
there. However, over the hemisphere n=ix+jy+kz so that V.n
becomes x^2. Thus the surface integral of x^2 taken over the
hemisphere just equals 2p/3=2.094395.
VOLUME OF A TETRAHEDRON VIA THE
DIVERGENCE THEOREM: Consider
the volume of a tetrahedron formed by the slanted plane
x+y+z=1 and the planes x=0, y=0 and z=0. We can obtain this
volume V quickly by applying the divergence theorem for the
vector field F=ix whose divF=1. One has V=Surface
Integral[ix.n dS]. This surface integral vanishes along
the x=0, y=0, and z=0 surfaces, leaving one with only
V=Surface Integral[ix.(i+j+k)/sqrt(3)dS]. Projecting dS into
the x,y plane via the substitution dS=dxdy/(n.k)=sqrt(3)dxdy,
one finds V=DoubleIntegral[xdxdy, over 0<y<(1-x),
0<x<1]=1/6. That is, the volume of the tetrahedron
formed by cutting a unit cube by a slanted plane passing
through three of its corners at (1,0,0), (0,1,0), and(0,0,1)
is just one-sixth of the cube volume.
 Introduction to matrices and matric multiplication.
Transpose and inverse of a matrix. Gauss-Jordan elimination
method. Solution of simultaneous algebraic and differential
equations by matrix methods. (Chapter 6)
Introduction to matrices and matric multiplication.
Transpose and inverse of a matrix. Gauss-Jordan elimination
method. Solution of simultaneous algebraic and differential
equations by matrix methods. (Chapter 6)
A QUICK TUTORIAL FOR
NUMERICAL MATRIX MANIPULATIONS USING MATLAB: One of the easiest to use canned programs
available for matrix calculations isMATLAB . Many of
you already own a student edition of MATLAB and the extended
version is also available in the Department's Computer Lab.
Here is a brief summary of what you can do-
1. First define a
Matrix, say: A=[3,4,5;
2,5,0;2,1,8] . Here element a2,3
in the second row and third column is 0.
2. The determinant is
found by typing: det(A) and for this matrix equals 16.
3. The inverse of A is
gotten by the operation: B=inv(A)
and here yields
[2.5,-1.6875,-1.5625;-1,0.875,0.625;-0.5,0.3125,0.4375].
4. Matrix multiplication
is defined by: A*B and, as expected, here yields the
identity(or unit) matrix I =[1,0,0;0,1,0;0,0,1].
5. The eigenvalues of
matrix A are given by: eig(A)
and here are found to be 0.2829,
10.1396, and 5.5775.
6. The corresponding
eigenvectors are obtained by: [V,D]=eig(A)
This prints out the three vectors
corresponding to the three different eigenvalues. Here we
find the three vectors are the transpose of
[-0.9048,0.3836,0.1848], [0.6457,0.2513,0.7210],and
[-0.2352,-0.8145,0.5304]. Note that one can always make one
of the elements of an eigenvector unity by multiplying all
elements in the vector by the same number.
USE OF MATRIX METHODS TO DEFINE A PLANE IN SPACE PASSING
THROUGH THREE POINTS: A very
nice application of matric methods is to find the equation for
the plane Ax+By+Cz=1 containing three specified points
P(x1,y1,z1),P(x2,y2,z2), and P(x3,y3,z3). Go HERE to see our
method for obtaining the values of A, B, and C using the
linalg portion of the canned math program MAPLE.
MATRIX MANIPULATOR
AVAILABLE ON THE WEB: To
quickly calculate the inverse, eigenvalues and determinent
values of matrices go to http://wims.unice.fr/wims/wims.cgi
.
4TH WEEK:(Chapters 3and part of 7)
 Eigenvalues, eigenvectors, and the fundamental
matrix. Incorporation of initial values and non-homogneous
terms into the matrix solution. A brief , easy to
grasp, one-page tutorial on basic matrix operations is found at
- http://www.math.hmc.edu/calculus/tutorials/matrixalgebra/
Eigenvalues, eigenvectors, and the fundamental
matrix. Incorporation of initial values and non-homogneous
terms into the matrix solution. A brief , easy to
grasp, one-page tutorial on basic matrix operations is found at
- http://www.math.hmc.edu/calculus/tutorials/matrixalgebra/
SAMPLE
CALCULATION FOR THE SOLUTION OF AN ODE BY MATRIX METHODS: We have shown in class how to reduce an nth
order ode to a set of first order equations expressible in
matric form as X'=MX. The eigenvalues k needed in the
solution follow from det[M-Ik]=0, where I is the unit matrix
I=[1,0,0;0,1,0;0,0,1]. Once the eigenvalue have been
determined one next constructs the eigenvectors X from the
recipe x1/cof(a11)=x2/cof(a12+x3/cof(a13+..where
the
cofactor cof(a)= (-1)^(i+j)*minor(aij) and i is the
row number, j the column number and the minor is that part of
the determinant left after one strikes out the row and column
containing the element aij. The final solution will
then be X=c1*X1*exp(k1*t)+c2*X2*exp(k2*t)
with
c1 and c2 being arbitrary constants and
k1 and k2 the two eigenvalues when
dealing with a second order ODE. Click HEREto see this solution procedure demonstrated
for a special case.
MULTIPLE MASS-SPRING
PROBLEM SOLVED BY MATRIX METHODS: An interesting application of the matrix
methods we have talked about in the last few lectures is the
determination of the eigenfrequencies of a multiple mass
spring system. One such problem is that shown HERE.For this problem the two equations of motion
are d2x1/dt2=-(k1/m1)x1+(k2/m1)(x2-x1)
and d2x2/dt2 = -(k3/m2)x2+(k2/m2)(x1-x2).
These
can be rewritten as four simultaneous first order ODEs whose
matrix form is as shown above. The eigenvalues and
corresponding eigenfunctions for this 4x4 coefficient matrix
are readily determined via the above matrix evaluation
link. We have carried out such an evaluation for m1=m2=1
and k1=k2=k3=1 and find the
eigenvalues to be ± i*sqrt(3)
and ± i. The corresponding
column eigenvectors read x1=[1,-1,sqrt(3),-sqrt(3)]
Tand x2=[1,1,0,0]T.
Thus one sees that the higher frequency mode consists of
the masses moving in opposite directions while the lower
frequency oscillation is characterized by the masses moving in
the same direction.
 More on the solution of dX/dt=M X , eigenvalues
and eigenvectors. Application of initial conditions. Solution of
non-homogeneous matrix equations by variation of parameters.
Phase plane techniques in connection with two simultaneous first
order differential equations.
More on the solution of dX/dt=M X , eigenvalues
and eigenvectors. Application of initial conditions. Solution of
non-homogeneous matrix equations by variation of parameters.
Phase plane techniques in connection with two simultaneous first
order differential equations.
5TH WEEK
 Review for the First Hour
In-Class Exam coming up later in the week.
Review for the First Hour
In-Class Exam coming up later in the week.
FIRST HOUR IN CLASS EXAM. Exam will cover material on vector fields and
matrix solution methods. Will be tested only on those topics
of Chapters 3, 6, 7, 8 and 9 discussed in class. Chapter 3
deals with converting higher order ODEs to matrix form , which
you should be able to do. The exam is closed book except you
can bring your calulator and one 3"x5" card containing
whatever you want to write on it. You can answer any three out
of four questions for a maximum of 10 points each. Partial
credit will be given .
6TH WEEK:
 Introduction
to Fourier Series( Chapter 10 ).
Representation of any bounded periodic function by an infinite
series involving sine and cosine terms. The Fourier
coefficients a n and b n. Several
examples of Fourier series.
Introduction
to Fourier Series( Chapter 10 ).
Representation of any bounded periodic function by an infinite
series involving sine and cosine terms. The Fourier
coefficients a n and b n. Several
examples of Fourier series.
WHO WAS JOSEPH FOURIER?- Jean Babtiste Joseph Fourier was a
mathematical physicist, teacher, revolutionary, politician ,
friend of Napoleon, and prefect of Grenoble. He was born in
Auxerre , France in 1768, the son of a tailor, and died in
Paris in 1830. He is today best known for the Fourier Series
and the Fourier Integral. He accompanied Napoleon on his
Egyptian campaign as scientific advisor, was for a short
time the governor of lower Egypt, and earlier almost lost
his head during the later stages of the French revolution
when he was accused of being a supporter of Robespierre ,
the most radical of the revolutionists. When Fourier first
submitted his paper on heat conduction and Fourier series to
the French Academy of Sciences in 1807, a panel consisting
of Laplace, Lagrange , Monge, Biot and others rejected the
paper as not being sufficiently rigorous. It was not until
1822 that this groundbraking work was published by Fourier
in bookform under the title "Theorie Analytique de la
Chaleur". The law of heat conduction( i.e. heat flow in a
solid conductor is directly proportional to the temperature
gradient ) is also named after him. The curly haired fellow
shown HERE
is J.Fourier.
SAMPLES OF FOURIER SERIES
FOR DIFFERENT PERIODIC FUNCTIONS: If you go HERE you will find applet animations
for five different periodic functions and how the Fourier
series approaches these as the number of terms increases
toward infinity. Note the Gibbs phenomenon at those points
where the functions have discontinuities.
 More on Fourier Series. Identities involving p. Expansion for even and odd functions.
Expansion for period p=2L. Parseval Identity.
More on Fourier Series. Identities involving p. Expansion for even and odd functions.
Expansion for period p=2L. Parseval Identity.
GENERATION
OF
FOURIER SERIES USING MATHCAD: HERE and HERE are
some examples of even Fourier series generated by Mathcad
including the one we spent a good portion of the period on
during the last lecture.
GENERATION
OF
FOURIER
SERIES USING MAPLE: We have
shown in class that that any function of period 2L can be
expanded in a Fourier series f(x)=(1/2)a 0+Sum[ancos(npx/L)+b n sin(npx/L), n=1..Infinity). Here an
=(1/L )*Int[f(x)*cos(npx/L),x=- L... L] and bn=(1/ L)*Int[f(x)*sin(npx/L), x=- L.. L]. One can easily automate this
procedure, as we have done in the attached jpg, by using the
canned program MAPLE. I show HEREthe plot of the Fourier series for
f(x)=[sin(x)] 5 for period 2p.
If you tried this by hand it would require considerable time.
Also, you will notice that, the series requires only 5 terms
n=1,...,5 to represent f(x) exactly. A second example consider
the odd function of period 4 whose value is zero for
0<x<1 and (x-1) for 1<x<2. It has only
nonvanishing bn coefficients and a Fourier series of 100 terms
produces the results shown HERE.As a
third example consider the use of MAPLE to obtain the Fourier
series for an even more complicated triangular periodic
function F(x)=0 for 0<x<2, =(x-2) for 2<x<3, and
=(4-x) for 3<x<4 where L=2. Here the function has
no symmetry and hence both the an and bn terms
are non-vanishing. The results of the MAPLE calculation are
shown HERE. Again to carry out such a calculation by
hand would be rather tedious.
REPRESENTING A PARABOLA BY
A FOURIER COSINE SERIES: If you
want to represent a non-peridic function F(x) by a Fourier
series, you can always do so by defining the range
-L<x<+L over which you want to represent the function. I
do this HERE by looking at F(x)=x2 in -p<x<p.
A simple evaluation yields the even Fourier series
representation
F(x)=p2/3+4*Sum[(-1)n*cos(nx)/n^2,
n=1..infinity]
for this case. As the graph shows, this peridic function
nicely represents the parabola F(x)=x2 inside
-L<x<+L but clearly does not do so outside. An
interesting equality which follows from this result (when one
sets x=0) is that p2/12=1-1/4+1/9-1/25+...
=0.8224670...Also
one could think of the periodic parabolic structure shown in
red as the shape of a reflecting surface capable of collecting
light, incoming parallel to the y axis, and concentrating the
radiation at the points (x, y)=(2pn,
1/4).
DIFFERENTIATION AND
INTEGRATION OF FOURIER SERIES: It
is possible to both differentiate and integrate the two sides
of a Fourier series and in most cases recover a correct form
for the resultant function. We demonstrate this HERE for the case of the discontinous function
f(x)=+1 for 0<x<1 and f(x)=-1 for -1<x<0 which has
a simple Fourier sine series representation. Note that an
integration yields a sawtooth function g(x) and a
differentiation yields a bunch of delta functions h(x).
Mathematicians tend to be very uncomfortable with
differentiating functions with discontinuities but as seen the
results aren't bad in this case and have the form of what is
expected by looking at the slope of the original function
f(x).
WHO WAS PARSEVAL?-Antoine Parseval(1755-1836) was a French
royalist jailed during the French Revolution and almost
beheaded. Later got in trouble for publishing an
anti-Napoleonic treatise and had to flee the country.
Published just five mathematical papers during his lifetime,
but these contained important new results including the
Parseval inequality and the Parseval theorem.
AN APPLICATION USING THE
PARSEVAL THEOREM: We
have shown in class that when squaring the Fourier series for a
function f(x) by itself and then integrating the result over the
range -L<x<+L, one arrives at the Parseval result
(1/L)*Int[f(x)2, x=-L..L)=(1/2)ao^2+Sum[an2+bn2,
n=0..infinity]]
, where an and
bn are the Fourier coefficients. This result can
be used, when f(x)=x and L=1, to show that the sum of the
reciprocals of the square of all integers equals p2/6=1.644934066848.. ( a
result already known to Euler prior to the invention of
Fourier series). The Parseval relation is one way to relate
certain definite integrals to an infinite series. Other
techniques exist including a very powerful approach using the
geometric series and Laplace transforms.
7TH
WEEK:
 Complex
Form of the Fourier Series, Development of the Fourier
Transform. The Dirac delta function and the Heaviside step
function and their Fourier transforms.
Complex
Form of the Fourier Series, Development of the Fourier
Transform. The Dirac delta function and the Heaviside step
function and their Fourier transforms.
WORKING WITH THE COMPLEX
VERSION OF THE FOURIER SERIES:
The standard Fourier series can readily be converted to its
complex form by using the substitutions
cos(x)=[exp(ix)+exp(-ix)]/2 and sin(x)=[exp(ix)-exp(-ix)]/2i.
This leads to f(x)=Sum[cn exp(inpx/L),
n=-infinity..infinity]
with
cn=[1/(2L)]*Int[f(x)*exp(-inpx/L,
x=-L..L].
Here L is the function half period and n represents all
integers. Applying this result to the repetative rectangular
pulse of period 2L=4 with f(x)=+1 for -1<x<+1 and f(x)=0
for -2<x<-1 and 1<x<2, we find that f(x)=Sum[1/(n*p)*sin(p/2)*exp(inpx/2),n=-infinity..+infinity]. This is
equivalent to f(x)=0.5+2*Sum[sin(np/2)*cos(npx/2)/(np),n=1..infinity].
Click
HEREto see an approximation of this last result
using a 200 term approximation. Note that the rectangular
pulse is nicely reproduced except for the unavoidable Gibbs
ear phenomenon at its discontinuities.
RELATION BETWEEN THE
FOURIER SERIES AND THE FOURIER TRANSFORM: A question which arises when studying Fourier
series of period 2L, is what happens when L is allowed to go
to infinity but the actual function f(x) has appreciable value
only near x=0. In this limit the summation in the Fourier
series goes over to an integral and one ends up with two
integrals , one giving the Fourier transform g(w) of the
function f(x) and the second the inverse which returns one to
the original function f(x). Such transforms are of tremendous
importance in numerous modern research areas and methods, such
as the FFT(Fast Fourier Transform ) , which aid in the
speeding up the Fourier transform process, are very much in
voque. The standard Fourier Transform of f(x) is given by g(w)=1/sqrt(2Pi)*Int[f(x)exp+iwx,
x=-infinity..+infinity] and its
inverse is f(x)=1/sqrt(2*Pi)*Int[g(w)exp(-iwx),
w=-infinity..+infinity].
Note many engineers use a less symmetric version of the
Fourier Transform Pair [f(x),g(w)] in which the integral for
f(x) is multiplied by one and the integral for g(w)by 1/(2Pi)
and the signs in the exponents may be switched. It makes no
difference as to which of these definitions is used as long as
one is consistent. To get some feel for the Fourier integral,
we look at the Fourier integral for the rectangular pulse
f(x)=1 for -1<x<1 , namely, (1/p)*Int[cos(kx)*sin(w)/w,
w=-N..N)
with
N->infinity. A numerical
approximation obtained via MAPLE using N=60 yields the result
shown HERE. A comparison with a standard Fourier series
expansion for the same function when the period is 2L=5 is
also shown and , as expected, the two results almost
coincide.
 Completion of Chapter 10. More on some manipulations
with Fourier Integrals. Also working out some problems from the
book involving both Fourier Series and Fourier Transforms.
Completion of Chapter 10. More on some manipulations
with Fourier Integrals. Also working out some problems from the
book involving both Fourier Series and Fourier Transforms.
FOURIER SINE TRANSFORM FOR
A TRIANGLE: Consider the triangle
function f(x)=x in -L<x<L. Its Fourier Sine Series is
readilly shown to be f(x)=Sum[b nsin(n p x/L), n=1..infinity], where b n=(2/L)*Int[f(x)*sin(n p x/L), x=0..L]. If we now let w=np /L so that dw=( p/L)dn
and
allow L to go to infinity, we can replace the Sum[( )dn by an
integral Int[( )L/ p)dw. This
results in a double integral with the integral limits on both
the variable w and x extending from 0 to infinity. We thus
have obtained the Fourier Sine Transform where the transform
of f(x) is defined as
g(w)=Int[f(x)*sin(wx),x=0..infinity] and its inverse is
f(x)=(2/ p)*Int[g(w)*sin(wx),
w=0..infinity]. Specifically , for the triangle function one
finds that g(w)=-cos(w)/w+sin(w)/w^2. Upon inverting,
this yields the result f(x)=(2/ p)*Int[(sin(w)/w^2-cos(w)/w)*sin(wx),
w=0..infinity]. We have plotted an approximation to this
integral HERE. Note that I have approximated w=0 by 0.001 to
avoid the singularity at w=0 and have replaced the upper limit
of infinity by w=200 to give a reasonable computer run time
when using MAPLE.
USING MAPLE OR MATLAB TO
FIND FOURIER TRANSFORMS:
Existing canned programs such as MAPLE or MATLAB can
very quickly calculate for you the Fourier transform g(w) of a
function f(x). We demonstrate this HERE
by showing some graphs of f(x) and the corresponding
transform.
USE OF FOURIER TRANSFORMS
IN RETURNING FILTERED SIGNALS: If
one treats the x as time t and the w as angular frequency w , then the Fourier transform g(w)
can be thought of as a frequency spectrum (decomposition) of
the original signal f(x). One can introduce some filtering
into this g(w) by multiplying it by a window function
H(x-a)-H(x-b), where H is the Heavyside step function. The
result, on inverting the product, produces an approximation to
the original f(x) which is missing those frequency components
outside the window. I demonstrate this HEREby looking at the inverse of the Fourier
transform of the square pulse f(x)=H(x-2)-H(x-3), when
filtered by the windows -5<w<5 and by
-50<w<50. You will note that a lot of information about
the detailed structure of f(x) is lost when inverse Fourier
transforming the filtered transform. On the other hand, when a
signal is received containing a lot of noise , use of
filtering can help bring about a clearer view of the original
signal. In connection with such filtered decompositions, I
also want to make you aware of the wavelet
approach to signal analysis.
This has become a very active area of applied
mathematics research in the last few years and is a serious
competitor to Fast Fourier Transform approaches for signal
compression and de-noising.
THE DIRAC DELTA FUNCTION
AND ITS FOURIER TRANSFORM: An
important function encountered in various applications
including mechanical vibrations, quantum mechanics, and
control theory is the Dirac delta function defined as d(x-a)=infinity at x=a and zero for all
other x. It has the further property that Int[d(x-a)*f(x),
x=-infinity..+infinity)=f(a). Note that the delta function
also equals the derivative of the Heaviside step function
H(x)=0 for x<a and H(x)=1 for x>a. The Fourier transform
of d(x-a) equals g(w)=Int[d(x-a)*exp(-i*w*x),
x=-infinity..+infinity]=exp(-i*w*a). Taking the inverse
Fourier transform of this result, we find another
representaion for the Dirac delta function , namely, d(x-a)=(1/p)*Int[cos(w*(a-x)),
w=0...+infinity]=sin(w*(x-a))/(p*(x-a)) . As an
approximation for the value of this last integral, we show you
HEREa plot of this integral for a=0 when the upper
limit on w is taken as w=10.
A TABLE OF FOURIER
TRANSFORM PAIRS: By going HEREyou
can
find a table of some of the better known Fourier transforms and
their inverses. We see, for example, that the gaussian
f(x)=ex[(-x2) has the transform g(k)=sqrt(p)*exp(-k2/4) and that the
function f(x)=Heaviside(x-0)*exp(-x) has the transform
g(k)=1/(1+I*k). From this last result at x=1 one can infer
(after a bit of manipulation which I leave as a challenge to the
reader) that int(w*sin(w)/(1+w^2), k=0..infinity)=p/(2*exp(1))=0.57786..Note that this last
value is close but not equal to the famous Euler-Mascheroni
constant g=0.577215...=lim n->
infinity[1+1/2+1/3+..+1/n-ln(n) ].
FOURIER TRANSFORM OF
CONVOLUTION INTEGRALS: We
showed in class that the Fourier transform of the
convolution integral f*g=Int[f(z)g(x-z),
z=-infinity..+infinity] equals sqrt(2Pi)*F(f(x))F(g(x)),
where F indicates the Fourier transform of the separate
functions. One can also invert this result to state that
(f*g)=F -1[ F(f(x))F(g(x))]. This last form can
help in the evaluation of some complicated integrals. We
demonstrate this HERE
for the case of
the rectangular pulse f(x)=+1 for -1<x<=1 and zero
everywhere else and the function g(x)=1/(1+x2
). After some manipulations( which I leave for the
reader to carry out), one finds in this case, that-
(1/2)
arctan(2/x2) =
Int[sin(w)cos(wx)exp(-w)/w, x=0..infinity]
from which also follows that
Pi/4=Int[(1/w)sin(w)exp(-x), x=0..infinity]
8TH WEEK:
 Introduction
to Partial Differential Equations.(
Chapter 11) . Formulation and Solution of the 1D Wave
Equation. Separation of Variables Solution Method and
d'Alembert's Solution.
Introduction
to Partial Differential Equations.(
Chapter 11) . Formulation and Solution of the 1D Wave
Equation. Separation of Variables Solution Method and
d'Alembert's Solution.
THE VIBRATING STRING
PROBLEM:- One of the best known
solutions of a partial differential equation is that for
a vibrating string of length L tied down at x=0 and x=L.
Here the PDE reads ytt =c2yxx
, where the subscripts indicate partial derivatives of the
transverse string displacement y(x,t) and c =sqrt(T/ r) is the constant speed of signal
propagation depending on the tension T and the string's linear
density r. The two boundary
conditions are y(0,t)=y(L,t) and the initial conditions are
y(x,0)= f(x) and yt
(x,0)= y(x). This equation can be
solved by a separation of variables approach y(x,t)=F(x)*G(t)
and use of the Fourier sine series. We show you HERE the solution obtained when L=1, c=1, f (x) =
sin(3 p x), and y (x)=0. For this case one finds the
standing wave form y(x,t)=cos(3 p
t)*sin(3 px) which has the fixed
angular frequency of w=3p. It is the uniqueness of the
vibration frequency for a string vibrating in a given
oscillation mode which makes stringed musical instruments
possible.
Another interesting solution of the vibrating string corresponds
to f(x)=x/Pi for 0<x<Pi/2 and f(x)=(1-x/Pi)
for Pi/2<x>Pi , with y(x)=0.
In this case the initial triangular displacement yields the
following pattern(HERE.) at later times.
 More on the Wave Equation and solution in Higher
Dimensions. Vibrating Membrane. Sound Waves in a Sphere.
Waveguide problem.
More on the Wave Equation and solution in Higher
Dimensions. Vibrating Membrane. Sound Waves in a Sphere.
Waveguide problem.
D'ALEMBERT'S SOLUTION OF
THE 1D WAVE EQUATION:-We have
shown in class that substitution of the characteristic
variables h =x-ct and x=x+ct converts the one
dimensional wave equation to y hx
=0 , which on simple integration yields the general solution
y(x,t)=f(x-ct)+g(x+ct). If one now considers a string of
infinite length and uniform density, one need only apply the
initial conditions y(x,0)= f (x)
and yt(x,0)= y(x) to
find the unique values of f and g. This is what D'Alembert did
(and also what we showed in class). The result is-
y(x,t)=[f(x-ct)+f(c+ct)]/2
+ [1/(2c)]*Int[ y ( m), m
=x-ct ...x+ct]
which is known as
D'Alembert's Solution. We show you HEREa picture of D'Alembert(1717-1783) and a
MATLAB created graph of the solution when initial conditions
are f=exp(-x^2) and y=0. Note that the initial gaussian
breaks up into two gaussians of half the original height and
that these travel in opposite directions at speed +c and -c
along the string. Another view of wave development for the
same initial Gaussian displacement is found by going HERE.
A VIBRATING RECTANGULAR MEMBRANE:- A good
demonstration of the solution of the wave equation in 2D is
that associated with a vibrating rectangular membrane. Here
the governing equation for the membrane displacement is
Ztt=c 2(Z
xx+Zyy) and one tries the separation of
variables substitution Z=T(t)*F(x,y)=T(t)sin(n p x/a)sin(n py/b),
assuming that the membrane is clamped at its edges at x=0,
x=a, y=0, and y=b. This leads to the double Fourier sine
series solution running over the integers n and m from 0 to
infinity. The imposed initial conditions F(x,y,0)= f(x,y) and Ft (x,y,0)= y (t) determine the values of
the constants Anm and B nm
appearing in T(t)=A nm sin( wt)+B nm cos( wt), where w
=c p *sqrt([(n/a)^2+m/b)^2]. The
spatial part of this solution, for a given n and m ,is
referred to as an eigenmode F(x,y) and the corresponding
angular frequency w is the
eigenfrequency. We show you HEREa MATLAB drawn 3D surface representing
Z(x,y,0) for n=4 and m=5 when a=b=1.
HOW TO USE MATLAB TO GRAPH SOLUTION SURFACES
U(X,Y): Some of you , who
have available computer programs such as MATHCAD, MAPLE,
MATHEMATICA, or MATLAB , have been asking me how one goes
about plotting some of the solution surfaces U(x,y) we have
been encountering in solving PDEs. I'll show you here one
example based on the solution of Uxx=Uxy subject to U(x,0)=x^2
and U(0,y)=sin(y). By the method of characteristics we know
the general solution to this PDE is U=F(y+x)+G(y) where the
functions F and G can be evaluated by use of the specified
boundary comditions. We find U(x,y)=sin(y)+2yx+x^2. A plot of this finction
is given
HERE.
9TH WEEK:
 Derivation and
Solution of the 1D Heat Conduction Equation.
Time-dependent development of temperature in a bar with zero end
temperatures but x dependent initial condition. Treatment of
heat conduction problems in bar with finite end temperatures. 1D
Diffusion problems.
Derivation and
Solution of the 1D Heat Conduction Equation.
Time-dependent development of temperature in a bar with zero end
temperatures but x dependent initial condition. Treatment of
heat conduction problems in bar with finite end temperatures. 1D
Diffusion problems.
TEMPERATURE IN A BAR:
The temperature T(x,t) in a bar of length L , and
maintained at zero end temperature, is governed by the 1D Heat
Conduction Equation T t =aTxx
subject to the IC of T(x,0)= f(x)
plus two BCs of T(0,t)=T((L,t)=0. As shown in class, this
equation can readily be solved by a separation of variables
approach by setting T(x,t)=G(t)*F(x). This leads to the result T(x,t)=Sum[C n *sin(n px/L)*exp(- a
(n p /L)^2*t), n=1..infinity] , where the coefficient Cn is
given by Cn=(2/L)*Int[f(x)*sin(n px/L),
x=0..L]. We show you HERE the
time development of this temperature profile when the bar has
an initial temperature of T(x,0)= f(x)=1
and length L=1. As expected, the temperature will be very
close to the end temperature by the time the non-dimensional
parameter a t/L 2
>1.
TIME-DEPENDENT TEMPERATURE
IN A SLAB: The time dependent
temperature in a slab (where 0<x<a, 0<y<b)
represents a good example of heat conduction in 2D. The
governing equation is Tt= a
(Txx+Tyy) and this has the very simple
separation of variables solution T(x,y,t)=DoubleSum[(1-(-1)^n)*(1-(-1)^m)*exp[- a*p^2*t*((n/a)^2+(m/b)^2)]*sin(n*p *x/a)*sin(m* p*y/b)/(n*m),
n=0..infinity,
m=0..infinity]
whenver the temperature
vanishes at the edge of the slab and the initial temperature
is T(x,y,0)=1. We show your HEREa 3D color plot of the temperature in the slab
at at/a^2=0.05 when a=b=1.
 Conduction
in bars of infinite length using the Fourier Integral approach.
The Error Function and its properties. Use of Laplace transforms
to solve the 1D heat conduction equation. Heat conduction in a
cylindrical geometry.
Conduction
in bars of infinite length using the Fourier Integral approach.
The Error Function and its properties. Use of Laplace transforms
to solve the 1D heat conduction equation. Heat conduction in a
cylindrical geometry.
ERROR FUNCTION: In solving the 1D heat conduction equation
over the infinite range -infinity<x<infinity one finds
that T(x,t)=1/(2sqrt( pa
t))*Int[T( x,0)*exp((x- x)^2/(4 at)),
x=-infinity...infinity] . For cases where the initial condition T(x,0)
is a constant over part of the x range and zero everywhere
else, this integral can be converted via the substitution
u=( x-x)/(2sqrt( at)) to an integral of the form erf(x)=[2/sqrt( p )]*Int[exp(-u^2),u=0..x)] . This last
integral is referred to as the error function and has the
property that erf(0)=0 and erf(infinity)=1. It is a
tabulated function and I show you its graph HERE
as obtained via MATLAB. The error function arises all the
time in both diffusion and conduction problems and so is one
you should be familiar with.
FOURIER TRANSFORM SOLUTION
FOR THE TEMPERATURE IN A BAR OF INFINITE LENGTH: The heat conduction equation in 1D when x
extends from minus to plus infinity can be conveniently solved
by Fourier transform methods. Applying the standard Fourier
transform to Tt=aTxx
yields df(k,t)/dt=-ak^2
f(k,t) where f(k,t) is the Forier transform of the unknown
temperature T(x,t). Solving we get f(k,t)=C(k)exp(-ak^2t), where C(k) is the Fourier
transform of the initial condition T(x,0).
Inverting f(k,t) leads to
the solution T(x,t). With a little manipulation this solution
can be written as-
T(x,t)=1/(2*sqrt(apt)*Int[T(z,0)*exp(-(z-x)^2/(4at)), z=-ininity...infinity] so that
the temperature will be known at all later time once T(x,0) is
specified. We show you HERE the solution for the case of an initial
temperature condition represented by the double pulse
T(x,0)=H(x+2)-H(x+1)+H(x-1)-H(x-2). The solution is
expressible exactly in terms of error functions or in terms of
the integral shown in the figure.
AGE OF THE EARTH:
An interesting heat conduction
problem concerns the cooling of a sphere of radius r=a and
an intial constant temperature T o. This is a
problem first looked at by Lord Kelvin in the 19th century
to determine the age of the earth. Casting the problem into
spherical coordinates one needs to solve Tt= a [Trr +(2/r)Tr]
subject to T(0,t) finite, T(a,t)=0, and T(r,0)=T o.
Using the substitution T=R(r)/r]exp(- al
2t), this leads to R"+l
2R=0. From this follows the closed form solution
T(r,t)=Sum[(2T oa/npr)(-1)n+1
sin(npr/a) exp( a(np/a)2t),
n=1..infinity]. We have plotted this result on the
accompanying graph for at=0.1,
0.5, and 1. The approximate e-folding time for the original
temperature is seen from this result to be t*=(a/ p )2/a.
Although Kelvin estimated from his solution (based on the
temperature rise in deep mines) that the earth was only some
24 million years old and this value is clearly in error as
pointed out by numerous sources at the time(Huxley etc), the
value of t*obtained for the earth ( assuming it to be made
essentially of iron where a=0.205cm
2/sec) is actually t*=(6.378x10 8cm/ p ) 2/0.205=2.01x10
17sec=6.38 billion years, which is in the right
ballpark for the earth's current estimated age of about 4
billion years and a bit higher than this value because of
the neglect of known convection which speeds up the heat
transfer process . Perhaps Kelvin's shorter cooling time
estimate was partially influenced by the Victorian belief
that , according to Bishop Usher(1581-1656) , the earth was
created precisely in 4004 BC. Also deep mine
temperatures are partially influenced by heating due to
radioactive decay and thus throw off his calculations.
10TH
WEEK
 Derivation of
the Laplace Equation. Dirichlet Solution in the Rectangle.
Application to Inviscid 2D Flow and Electrostatics.
Derivation of
the Laplace Equation. Dirichlet Solution in the Rectangle.
Application to Inviscid 2D Flow and Electrostatics.
WHO WAS LAPLACE?- Pierre Simon de Laplace(1749-1827) was a
French Astronomer and Mathematician with many scientific
credits to his name. He proposed the nebular theory of the
evolution of the solar system, introduced the concept of a
potential , was involved in setting up the metric system, did
work on probability, wrote a monumental multi-volume work on
planetary mechanics entitled "Traite du Mecanique Celeste"and
proved (the obvious) that the solar system is stable. He was
also very adept at always allying himself with the "in"
political powers throughout his lifetime. He was a member of
the French Academy of Sciences , taught at the Ecole Normal in
Paris, and was made Count of the Empire and Chancellor of the
Senate by Napoleon(although he was removed from this last post
after only six weeks because of his tendency to micro-manage
things). Laplace became a marquis after restoration of the
Bourbons in 1817. He was also a friend (and later enemy)of
Benjamin Thompson(alias Count Rumford), the famous American
Tory who fled to England during the American revolution and
later became well known in scientific circles for his
mechanical equivalent of heat measurements while observing the
boring of cannons for the elector of Bavaria.
A picture of Laplace is found HERE.
SOLUTION OF THE LAPLACE
EQUATION IN A SQUARE FOR DIRICHLET BOUNDARY CONDTIONS- One can solve the 2D Lapace equation for a
rectangular cartesian geometry and for Dirichlet bcs by a
simple separation of variables and superposition approach. As
an example of this consider the solution when V(x,y) satisfies
the boundary conditions V(0,y)=V(1,y)=1 and V(x,0)=V(x,1)=0.
Here one superimposes the solution corresponding to the bc's
V(0,y)=V(x,0)=V(x,1)=0 and V(1,y)=1 onto the solution
satisfying the bcs V(1,y)=V(x,0)=V(x,1)=0 and V(0,y)=1. This
leads to-
V(x,y)=(2/p)*Sum{(1-(-1)^n)/(n*sinh(n* p))*[sinh(n*p*x)+sinh(n* p*(1-x))]*sin(n*p*y),
n=1..infinity}
A graph for the contours V(x,y)=Const. predicted
by this solution is found by going HERE.
SOLUTION
OF
THE LAPLACE EQUATION INSIDE A CIRCLE: Another
interesting problem concerns the value of the electric potential
V inside a circle of radius r=a when the boundary condition V(a,q)=f(q) is
specified. Here the appropriate PDE is (Vrr+(1/r)Vr+(1/r^2)Vqq=0 and a separation of
variables solution yields
V(r,q)= Sum[(r/a)^n (Ansin(nq)+Bn cos(nq),
n=0..infinity]
where An and Bn are constants to be
evaluated from the bc at r=a. We show you HERE a graph of the
solution V(r,q)=1/2-1/2(r/a)2cos(2q) found when f(q)=
sin(q)2=(1/2)*(1-cos(2q). Note that V equals its mean value of
0.5 along the two diagonal lines where cos(2q)=0.
OCCURRENCE
OF BESSEL FUNCTIONS: When dealing with the solutions of the wave or heat
conduction equation in polar coordinates or Laplace's
equation in cylindrical coordinates with a z variation
, one finds that the radial part of the solution involves
Bessel functions of the first kind in the form Jm(umn
r/a) , where umn is the nth zero of the mth order
Bessel function and r=a is the radius of the circular
boundary. For example, the wave equation for a vibrating
circular membrane of radius r=a has the solution
U(r,theta,t)=G(t)*F(r,theta), where G(t)=Asin(wt)+Bcos(wt)
and F(r,theta)=Jm(umnr/a)*[Csin(m
theta)+Dcos(m theta)]. Here A,B,C,and D are constants which
can be evaluated by the given initial values and the
boundary condition at r=a , w=umnc/a is the
angular frequency, and c the propagation speed. The product
G*F is double summed over the integer values of n and m. We
show you HERE a
graph of a typical non-axisymetric eigenfunction Fmn=F1,2
encountered in such a solution.
By going HERE you
will find the important orthogonality property for Bessel
functions which allows one to expand any bounded functions
in terms of a Fourier-Bessel series.
 REVIEW FOR SECOND HOUR EXAM , including
going over some exam questions from previous years. Topics to
be covered on the exam will be Fourier series and transforms ,
and the solution of PDE's , including the wave, heat
conduction, and Laplace equations.
REVIEW FOR SECOND HOUR EXAM , including
going over some exam questions from previous years. Topics to
be covered on the exam will be Fourier series and transforms ,
and the solution of PDE's , including the wave, heat
conduction, and Laplace equations.
11TH WEEK:
 SECOND HOUR EXAM. Closed book except you can bring one 3"x5" card and
your hand calculator.
SECOND HOUR EXAM. Closed book except you can bring one 3"x5" card and
your hand calculator.
 Introduction to Complex Variables. Cartesian and polar
representations of a complex number and its Argand diagram
representation. Addition, subtraction , multiplication and
division. DeMoivre Formula for finding multiple roots of complex
numbers.
Introduction to Complex Variables. Cartesian and polar
representations of a complex number and its Argand diagram
representation. Addition, subtraction , multiplication and
division. DeMoivre Formula for finding multiple roots of complex
numbers.
ARGAND DIAGRAM- This is a convenient way to plot a complex
number z=x+iy within the z plane. The x axis represents the
real part of z and the y axis the imaginary part. In polar
form one has z=r exp(i q ), so that
r=sqrt(x^2+y^2)=amp(z) and q
=arctan(y/x)=arg(z) is the angle measured in the
counterclockwise sense. Click HEREto see the location of the complex number
z=exp(i q) at intervals of d q = p/4
starting with q=0.
WHO WAS DE MOIVRE? -Abraham de Moivre(1667-1754) was French born
protestant who emigrated to England after the revocation of
the Edict of Nantes and during the expulsion of all Huguenots
from France. He was unable to obtain a university position in
England as a foreigner and had to maintain himself as a tutor
of mathematics. He wrote several books in the area of analytic
geometry, probability, and statistics and was a member of the
Royal Society and a friend of Newton. He discovered the
Stirling formula before Stirling and is today mainly
remembered for his formula for obtaining the roots of a
complex number.
USE OF COMPLEX VARIABLE METHODS TO QUICKLY OBTAIN TRIGNOMETRIC
IDENTITIES: We can use
complex variable methods to obtain some of the trignometric
identities you encountered in some of your earlier math
classes. The key
for doing so is the Euler Identity exp(iz)=cos(z)+isin(z). Go
HERE to see
some of these identities derived.
PROPERTIES OF
COMPLEX HYPERBOLIC FUNCTIONS: In discussing functions of complex variables one often
runs into the hyperbolic functions sinh(z), cosh(z) etc. The
properties of such functions are easily established by
replacing z by x+iy. Thus , for example,
sinh(x+iy)={exp(x)[cos(y)+isin(y)]-exp(-x)[cos(y)-isin(y)]}/2=cos(y)sinh(x)+isin(y)cosh(x)
,
so that sinh(1+i)=0.63496..+i 1.2984.. . In case you are a
little rusty on hyperbolic functions go
HERE to
refresh your memory.
THE COMPLEX
NUMBER Z=(1+I)^n AND THE BERNOULLI SPIRAL: Sometimes powers of complex numbers lead to
very interesting trajectories in the Argand plane as the power
is varied continiously. Take, for example, the number
Z=(1+i)^n and let n vary from n=0 to infinity. It is clear
that Z=2i when n=2 and Z=-4 when n=4. Casting the number into
polar form we find that Abs(z)=r=2^(2 q/p)
and Arg(z)= q=n p /4. One can eliminate the n from
these last two results to find r=exp[2ln(2) q/p ] which is recognized to be a
standard Bernoulli logarithmic spiral . Click HEREto see its form. So what is the value of
(1+i)^16 ? J.Bernoulli was so proud of his discovery of
the logarithmic spiral r=a*exp(b*q )that
he had it inscribed on his tombstone. The engraver got the
figure slightly wrong and it rather looks like a bunch of
concentric circles. Click HERE to
see me pointing to the engraving of the spiral on a recent
visit to Basel, Switzerland.
MNEMONIC FOR THE NUMBER
EXP(1): As you know there are an
infinite number of irrational numbers arising in mathematics.
The most famous of these are e, p
and sqrt(2). Approximations to these numbers can be readily
retained by the use of mnemonics. Usually the mnemonics are
generated by counting the number of letters in a word. Thus
for example p="How I like a drink,
alcoholic of course, after the heavy lectures involving
quantum mechanics"=3.14259265358979. A shorter mnemonic for p is"May(3) I(1) have(4) a(1) small(5) container(9) of(2) coffee(6)".You can also construct a mnemonic using
other knowledge involving dates etc . I show you HEREa way to do this to 30 place accuracy for my
favorite irrational number e.
AN INTERESTING ITERATION
PATTERN GENERATED BY A COMPLEX NUMBER: Another interesting pattern involving a
complex number in the Argand Plane( and one I have not seen
before) is that obtained by the iteration a[n+1]=i^a[n]starting
with a[0]=0 . We get a[1]=i^0=1, a[2]=i^1=i,
a[3]=i^i=exp(- p/2),etc. We have
automated this iteration procedure with a one line MAPLE
program and have plotted the results HERE for the first 40 iterations. Notice the
interesting three arm spiral pattern generated with the large
n limit given by a[n]=i^a[n] whose solution can be expressed
in terms of the Lambert function and reads a[infinity]=(2i/ p )*Lambert( p/2i)=0.43828..+i*0.36059..
ROOTS OF ALGEBRAIC
EQUATIONS: It is known that an nth order algebraic
equation has n roots some of which may be real and others
complex. Thus for example the second order equation ax2+bx+c=0
can be written as (ax2+bx+b2/4a)=b2/4a-c
or
x=[-b +- sqrt(b2-4ac)]/(2a). Thus if a, b, and c are
real numbers, then the two roots are real if b2>4ac
and complex conjugates if b2<4ac. For the cubic
equation ax3+bx2+cx+d=0 things are a bit
more complicated. We show you HERE
its analytic solution based on some algebraic manipulations. It
is also possible to analytically solve the quartic algebraic
equation in closed form but not the quintic and beyond. For the
roots of higher order algebraic equations it is best to simply
used a canned numerical program . For example, using MAPLE,
the four roots of x4-x2+x-1=0 are
the two real values x= 1 and x= -1.465571232, and the two
complex conjugate roots x=0.2327856159-.7925519930 I and
x= 0.2327856159+.7925519930 I . According to the Descartes Rule
an algebraic equation has its number of positive roots equal to
the number of sign changes or less by an even integer. In the
last example we have three sign changes so that the number of
positive real roots are either 3 or 1. As seen the number is one
root in this case.
12TH WEEK
 Defining the
function of a complex variable f(z)=u+iv. Cauchy-Riemann
conditions for analytic functions. Some identities involving
complex variables. Orthogonality of the curves u=const. and
v=const. Complex velocity potential and some simple 2D inviscid
flows described by it.
Defining the
function of a complex variable f(z)=u+iv. Cauchy-Riemann
conditions for analytic functions. Some identities involving
complex variables. Orthogonality of the curves u=const. and
v=const. Complex velocity potential and some simple 2D inviscid
flows described by it.
DEMONSTRATION OF THE
ORTHOGONALITY OF THE u=Const and v=const CURVES: We have shown in class that for any
analytic function f(z)=u+iv, the curves u=const and
v=const form an orthogonal set of curves. Lets demonstrate
this fact for the function
f(z)=z*sin(z)=[xsin(x)cosh(y)-ycos(x)sinh(y)]+i[xcos(x)sinh(y)+ysin(x)cosh(y)].
The
contour map obtained via MAPLE in -4<x<4,-4<y<4
can be found by clicking HERE.
 More on functions of a complex variable. Complex
electrostatic and velocity potentials. Line integrals in the
complex z plane. Cauchy's Theorem.
More on functions of a complex variable. Complex
electrostatic and velocity potentials. Line integrals in the
complex z plane. Cauchy's Theorem.
ELECTROSTATIC POTENTIAL
USING COMPLEX VARIABLE METHODS: We
know that the 2D electrostatic potential V(x,y) in a vaccuum
is given mathematically by solving the Laplace equation .
Since both u and v of any analytic function f=u+i*v also
satisfy the Laplace equation, one can define a complex
electrostatic potential as F(z)=V(x,y)+iE(x,y) and consider
the real part of any analytic function f(z) to be a possible
solution for V(x,y) in a 2D electrostatic problem. We
demonstrate this HERE for the potential between two parallel wires
maintained at different constant potentials using the complex
potential function F(z)=ln(z-1)-ln(z+1). There are an infinite
number of other complex harmonic functions F(z), some of which
can also be used directly to describe electrostatic problems
for specified boundary conditions.
STREAMFUNCTION AND
VELOCITY POTENTIAL USING COMPLEX VARIABLE METHODS: A
2D inviscid flow is characterized by having a velocity field
(U,V) having both zero divergence and zero curl. This allows
the definition of a complex velocity potential F(z)=j(x,y)+iy(x,y),
where y is the streamfunction
satisfying U=yy and V=-yx
and j is the velocity potenetial
satisfying U=jx and V=jy.
Thus any analytic function f(z) can be considered to
represent a possible 2D flow field. Certain forms have
particular utility such as F(z)=±(Q/2p)ln(z),
F(z)=±i(G/2p)ln(z), and F(z)=k/z which
represent a source or sink, a clockwise or counterclockwise
rotating vortex, and a doublet, in that order. We show you HERE
the flow field created by superimposing a rectlinear flow
F(z)=z and a doublet F(z)=1/z. The streamfunctions(in green)
here are given by
y= Im(z+1/z)= (r-1/r)sin(q)
and the velocity potentials(in red) as j=Re(z+1/z)=(r+1/r)cos(q).
The resultant pattern corresponds to inviscid flow about a
cylinder.
WHO WAS CAUCHY?
-Baron Augustin Louis Cauchy(1789-1857) was one of the most
prolific mathematicians ever having written a total of 789
mathematical papers during his lifetime. His contributions
spread over many branches of mathematics and he is especially
known for development of the theory of complex variables. The
Cauchy-Riemann conditions and the Cauchy integral theorem are
named after him. He taught at the Ecole Polytechnique and the
Sorbonne plus spent some time teaching in Turin and Prague. He
won the Grand Prix of the French Academy of Sciences in 1816,
helped Napoleon with the invasion plans for England(1810), was
not well liked by his colleagues, and remained an ardent
royalist for most of his life.(Lucky for him that he was only
four years old during the reign of terror. The great French 51
year old chemist and discoverer of oxygen, Lavoisier, was not as
fortunate). A picture
of Cauchy is found HERE.
PROOF OF CAUCHY'S THEOREM:
A complex function f(z)=u+iv is
said to be analytic and hence have a unique derivative if it
satisfies the Cauchy-Riemann conditions that u x =vy
and v x =-u y . Let us now use these
properties to prove Cauchy's famous theorem that the line
integral around any closed curve in the z plane of f(z) is
zero provided this function is analytic within C. The proof is
based on Green's Theorem. We know from it that the double
integral of (v x + uy) equals the line
integral of (udx -vdy) around curve C. Likewise the double
integral of ( u x -v y )corresponds to
the line integral of (vdx +udy) around C. But since both of
these double integrals vanish by the Cauchy-Riemann conditions
, the line integral around C of
f(z)dz=(u+iv)(dx+idy)=(udx-vdy)+i(vdx+udy) must be zero. QED.
13TH WEEK
 Cauchy
Integral formula. Taylor series expansions. Residues.
Cauchy
Integral formula. Taylor series expansions. Residues.
EVALUATION OF A CLOSED LINE
INTEGRAL FOR A FUNCTION WITH HIGHER ORDER POLES: We have shown in class how to evaluate closed
line integrals involving functions with simple poles by means
of the residue theorem. This residue approach continues to
work for functions with higher order poles but in this latter
case the evaluation of the residue involves a more complicated
formula not worth committing to memory. Rather, it is better
to make use of the extended Cauchy integral for such a higher
order pole case. Let us demonstrate. Take the closed line
integral K=Int[exp(z)/(z-1)3]. In this case the
function f(z)=exp(z)/(z-1)3 has a third order pole
at z=1, so treating the integral by the Cauchy integral
formula we have K=(2pi/2!)[exp(z)]"
with the second derivative evaluated at z=1. We thus find K=i*pi*e.
 More on Taylor expansions. Laurent series and the
Residue Formula.
More on Taylor expansions. Laurent series and the
Residue Formula.
HOW TO FIND A RESIDUE:
In our discussions of solving closed line integrals in the
complex plane where f(z)=g(z)/h(z) , with g(z) being analytic
but h(z) having an n'th order zero at z=zo , we
expanded the top and bottom term in a Taylor series about z=zo.
This leads to
f(z)=g(zo)+g(zo)'(z-zo)+../h(zo)'(z-zo)+[h(zo)"/2!](z-zo)^2+
with all terms in the h(z) expansion vanishing before the nth
derivative term. We know that the only term in this quotient
which yields a non-zero value when integated around closed curve
about z=zo, is the one which goes as A/(x-xo) and that this term
integrates to 2*Pi*i*A. Thus by definition, the residue Res will
be A and we can conclude that for the
special case of a first order pole (n=1) the residue is just
Res=g(zo)/h(zo)' . For f(z)s with second and higher
order poles, more complicated expressions for the residue exist.
It is , however, more convenient in those instances to use the
Cauchy Integral Formula for nth order poles directly.
14TH WEEK
 Evaluation of
real integrals using complex variable methods. Filling out of
teacher and course evaluation forms.
Evaluation of
real integrals using complex variable methods. Filling out of
teacher and course evaluation forms.
EVALUATION OF A REAL
INTEGRALS BY RESIDUE METHODS: Click HEREandHERE. Also consider the integral J=Int[sin(t)4,
t=0..2p]. If we convert it via the
substitution z=exp(it) so that dz=izdt, we get the equivalent
closed line integral Int[(z2-1)4/(16iz5)]
around the unit radius circle about the origin. This can be
evaluated via the Cauchy integral formula to yield (2p)/(4!16)[d4((z2-1)4)/dz4] at z=0. Thus J=3p/4, a well known result.
 Review for the Third Hour Exam .
Review for the Third Hour Exam .

15TH WEEK:
 THIRD HOUR EXAM
covering everything in the complex variable area including
those parts of Chapters 12 through 16 discussed in class. The
exam will be closed book but you can bring one 3x5"card and
your calculator.
THIRD HOUR EXAM
covering everything in the complex variable area including
those parts of Chapters 12 through 16 discussed in class. The
exam will be closed book but you can bring one 3x5"card and
your calculator.
Your
final
course grade , composed of 90% for the three tests plus 10% for
the homeworks, will be normalized to a maximum score of
100. The grade breakup will be approximately as follows:
90<A<100, 88<B+<90,
80<B<88, 78<C+<80, 67<C<78, 62<D+<67,
51<D<62.
PHOTO OF OUR FALL
1998 EGM4313 CLASS:

Picture was taken with our old sub-megapixel
digital camera and hence the poor resolution . Class is standing
by the Stonehenge Sculpture behind the New Engineering Building.

Links
to our other Web Pages:
STRENGTH
MATHFUNC
DYNAMICS
STATICS
HOMEPAGE RESEARCH
To keep
your mind sharp you might want to prove some of the following
mathematical identities based on your knowledge of elementary
mathematics:
(1)-
Sum[n^6*exp(-nx), n=1..inf.]={sinh(x)*[cosh(x)^2 +
28*cosh(x) +61 ]}/{2[cosh(x)-1]^4}
(2)- Pi=48*arctan(1/38)+80*arctan(1/57)+28*arctan(1/239)+96*arctan(1/268)
(3)-
Iteration
a n+1 =exp( ia n ) starting with a1=1
converges to a=x+iy= 0.576412727399..
+i
0.374699027157.. as n goes to infinity. Here x follows from
[x/cos)x)]^2=exp-2[x*tan(x)] and y=x*tan(x)
(4)- Int[t^2*sin(t)/(exp(Pi*t)-1),t=0..inf.] =
1+coth(1)-coth(1)^3
(5)- Pi=
12*arcsin[sqrt(C)/2]=(6sqrt(C)*Sum[{(2n)!*(C/16)^n}/{(n!)^2*(2n+1)},
n=0..inf.] , where C=2-sqrt(3)
(6)-
Pi=24 arctan(B), where B=2*sqrt[2+sqrt(3)]-[2+sqrt(3)]
which can be written as the continued
fraction-
Pi=24sqrt(B)/{1+B/(3-B+9B/(5-3B)+25B/(7-5B)+..} and yields Pi good
to eleven
places
by taking terms up to 81B/(11-9B) into account.
(7)-
Sum[(n^2-1)/(n^2+1)^2,
n=1..inf]=[1-Pi^2*csch(Pi)^2]/2=0.443959960..
(8)-
csch(x)^2=1/x^2-2*Sum[((n*Pi)^2-x^2)/((n*Pi)^2+x^2)^2,n=1..inf]
(9)-
Sum[1/(n^2+a^2)^2,
n=-inf..+inf]=[Pi^2/(2*a^2)]*[csch(Pi*a)^2+coth(Pi*a)^2/(Pi*a)]
(10)-Prove
that
tan(54°)=(1/5)*{sqrt[10+2*sqrt(5)]+sqrt[5+2*sqrt(5)]}. Hint-work
with a regular pentagon with sides of length one.
(11)-The
area
of a regular decahedron , each of whose ten sides equal
unity, is A=2.5*sqrt[5+2*sqrt(5)]. Also one has that
(f^2-1/4) < A/Pi <
f^2, where f=(sqrt(5)+1)/2=1.608339.. is the golden ratio.
(12)-The odd number
2^(2n+1) +1 will be composite(ie.-non-prime) for all positive
integer values of n.
(13)-The value of Pi is given exactly by
Pi=4*int[1/sqrt((1-t^2)(2-t^2),
t=0..1]*int[sqrt(1-t^2)/sqrt(2-t^2), t=0..1)] .
Your PC can
readily confirm that these results are correct, but to
come up with a derivation or proof is a bit more
challenging.
Finally, look at the following graph. Notice anything
peculiar about it. Think number theory.
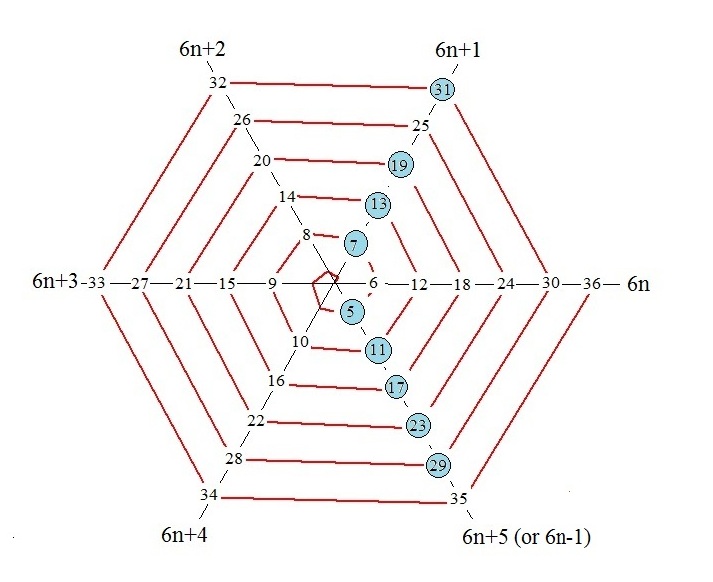
Latest update: July 28, 2016






![]()
![]()

 Today will be our first
lecture in EGM 4313. We will devote the time to a review of
vectors, talking about dot and cross products , the scalar and
vector triple. What we mean by scalar and vector fields, and
introduce the directional derivative and the gradient. (Chapter 8)
Today will be our first
lecture in EGM 4313. We will devote the time to a review of
vectors, talking about dot and cross products , the scalar and
vector triple. What we mean by scalar and vector fields, and
introduce the directional derivative and the gradient. (Chapter 8)  More on the gradient and the directional
derivative. Length of a Space Curve. Also concept of the
divergence of a vector and the curl of a vector. Some vector identities involving these three
operations.
More on the gradient and the directional
derivative. Length of a Space Curve. Also concept of the
divergence of a vector and the curl of a vector. Some vector identities involving these three
operations.  Expression of grad,div and curl in other
orthogonal coordinate systems.Vector manipulations used
to formulate equations of electromagnetic wave propagation, heat
flow, and 2D incompressible and inviscid fluid flow behaviour.
Line integrals and independence of path.
(End of Chapter 8 and beginning of Chapter 9)
Expression of grad,div and curl in other
orthogonal coordinate systems.Vector manipulations used
to formulate equations of electromagnetic wave propagation, heat
flow, and 2D incompressible and inviscid fluid flow behaviour.
Line integrals and independence of path.
(End of Chapter 8 and beginning of Chapter 9)
 Line Integrals
and Surface Integrals. Derivation and application of the
Divergence(Gauss)
Line Integrals
and Surface Integrals. Derivation and application of the
Divergence(Gauss) Green's
Theorem as a special case of Stokes Theorem. Green's Theorem
used to determine the areas bounded by various curves including
the cardiod. Also the derivation of Green's first and second
formulas from the divergence theorem. Evaluation of Surface
Integrals.Evaluation of some problems from
the book.
Green's
Theorem as a special case of Stokes Theorem. Green's Theorem
used to determine the areas bounded by various curves including
the cardiod. Also the derivation of Green's first and second
formulas from the divergence theorem. Evaluation of Surface
Integrals.Evaluation of some problems from
the book.  Introduction to matrices and matric multiplication.
Transpose and inverse of a matrix. Gauss-Jordan elimination
method. Solution of simultaneous algebraic and differential
equations by matrix methods. (Chapter 6)
Introduction to matrices and matric multiplication.
Transpose and inverse of a matrix. Gauss-Jordan elimination
method. Solution of simultaneous algebraic and differential
equations by matrix methods. (Chapter 6)
 Eigenvalues, eigenvectors, and the fundamental
matrix. Incorporation of initial values and non-homogneous
terms into the matrix solution. A brief , easy to
grasp, one-page tutorial on basic matrix operations is found at
- http://www.math.hmc.edu/calculus/tutorials/matrixalgebra/
Eigenvalues, eigenvectors, and the fundamental
matrix. Incorporation of initial values and non-homogneous
terms into the matrix solution. A brief , easy to
grasp, one-page tutorial on basic matrix operations is found at
- http://www.math.hmc.edu/calculus/tutorials/matrixalgebra/
 More on the solution of dX/dt=M X , eigenvalues
and eigenvectors. Application of initial conditions. Solution of
non-homogeneous matrix equations by variation of parameters.
Phase plane techniques in connection with two simultaneous first
order differential equations.
More on the solution of dX/dt=M X , eigenvalues
and eigenvectors. Application of initial conditions. Solution of
non-homogeneous matrix equations by variation of parameters.
Phase plane techniques in connection with two simultaneous first
order differential equations.
 Review for the First Hour
In-Class Exam coming up later in the week.
Review for the First Hour
In-Class Exam coming up later in the week.  Introduction
to Fourier Series( Chapter 10 ).
Representation of any bounded periodic function by an infinite
series involving sine and cosine terms. The Fourier
coefficients a n and b n. Several
examples of Fourier series.
Introduction
to Fourier Series( Chapter 10 ).
Representation of any bounded periodic function by an infinite
series involving sine and cosine terms. The Fourier
coefficients a n and b n. Several
examples of Fourier series.  More on Fourier Series. Identities involving p. Expansion for even and odd functions.
Expansion for period p=2L. Parseval Identity.
More on Fourier Series. Identities involving p. Expansion for even and odd functions.
Expansion for period p=2L. Parseval Identity.  Complex
Form of the Fourier Series, Development of the Fourier
Transform. The Dirac delta function and the Heaviside step
function and their Fourier transforms.
Complex
Form of the Fourier Series, Development of the Fourier
Transform. The Dirac delta function and the Heaviside step
function and their Fourier transforms.  Completion of Chapter 10. More on some manipulations
with Fourier Integrals. Also working out some problems from the
book involving both Fourier Series and Fourier Transforms.
Completion of Chapter 10. More on some manipulations
with Fourier Integrals. Also working out some problems from the
book involving both Fourier Series and Fourier Transforms.
 Introduction
to Partial Differential Equations.(
Chapter 11) . Formulation and Solution of the 1D Wave
Equation. Separation of Variables Solution Method and
d'Alembert's Solution.
Introduction
to Partial Differential Equations.(
Chapter 11) . Formulation and Solution of the 1D Wave
Equation. Separation of Variables Solution Method and
d'Alembert's Solution.  More on the Wave Equation and solution in Higher
Dimensions. Vibrating Membrane. Sound Waves in a Sphere.
Waveguide problem.
More on the Wave Equation and solution in Higher
Dimensions. Vibrating Membrane. Sound Waves in a Sphere.
Waveguide problem.  Derivation and
Solution of the 1D Heat Conduction Equation.
Time-dependent development of temperature in a bar with zero end
temperatures but x dependent initial condition. Treatment of
heat conduction problems in bar with finite end temperatures. 1D
Diffusion problems.
Derivation and
Solution of the 1D Heat Conduction Equation.
Time-dependent development of temperature in a bar with zero end
temperatures but x dependent initial condition. Treatment of
heat conduction problems in bar with finite end temperatures. 1D
Diffusion problems.  Conduction
in bars of infinite length using the Fourier Integral approach.
The Error Function and its properties. Use of Laplace transforms
to solve the 1D heat conduction equation. Heat conduction in a
cylindrical geometry.
Conduction
in bars of infinite length using the Fourier Integral approach.
The Error Function and its properties. Use of Laplace transforms
to solve the 1D heat conduction equation. Heat conduction in a
cylindrical geometry.  Derivation of
the Laplace Equation. Dirichlet Solution in the Rectangle.
Application to Inviscid 2D Flow and Electrostatics.
Derivation of
the Laplace Equation. Dirichlet Solution in the Rectangle.
Application to Inviscid 2D Flow and Electrostatics.  REVIEW FOR SECOND HOUR EXAM , including
going over some exam questions from previous years. Topics to
be covered on the exam will be Fourier series and transforms ,
and the solution of PDE's , including the wave, heat
conduction, and Laplace equations.
REVIEW FOR SECOND HOUR EXAM , including
going over some exam questions from previous years. Topics to
be covered on the exam will be Fourier series and transforms ,
and the solution of PDE's , including the wave, heat
conduction, and Laplace equations.  SECOND HOUR EXAM. Closed book except you can bring one 3"x5" card and
your hand calculator.
SECOND HOUR EXAM. Closed book except you can bring one 3"x5" card and
your hand calculator.  Introduction to Complex Variables. Cartesian and polar
representations of a complex number and its Argand diagram
representation. Addition, subtraction , multiplication and
division. DeMoivre Formula for finding multiple roots of complex
numbers.
Introduction to Complex Variables. Cartesian and polar
representations of a complex number and its Argand diagram
representation. Addition, subtraction , multiplication and
division. DeMoivre Formula for finding multiple roots of complex
numbers.  Defining the
function of a complex variable f(z)=u+iv. Cauchy-Riemann
conditions for analytic functions. Some identities involving
complex variables. Orthogonality of the curves u=const. and
v=const. Complex velocity potential and some simple 2D inviscid
flows described by it.
Defining the
function of a complex variable f(z)=u+iv. Cauchy-Riemann
conditions for analytic functions. Some identities involving
complex variables. Orthogonality of the curves u=const. and
v=const. Complex velocity potential and some simple 2D inviscid
flows described by it.  More on functions of a complex variable. Complex
electrostatic and velocity potentials. Line integrals in the
complex z plane. Cauchy's Theorem.
More on functions of a complex variable. Complex
electrostatic and velocity potentials. Line integrals in the
complex z plane. Cauchy's Theorem.  Cauchy
Integral formula. Taylor series expansions. Residues.
Cauchy
Integral formula. Taylor series expansions. Residues.
 More on Taylor expansions. Laurent series and the
Residue Formula.
More on Taylor expansions. Laurent series and the
Residue Formula.  Evaluation of
real integrals using complex variable methods. Filling out of
teacher and course evaluation forms.
Evaluation of
real integrals using complex variable methods. Filling out of
teacher and course evaluation forms.
 Review for the Third Hour Exam .
Review for the Third Hour Exam . 
 THIRD HOUR EXAM
covering everything in the complex variable area including
those parts of Chapters 12 through 16 discussed in class. The
exam will be closed book but you can bring one 3x5"card and
your calculator.
THIRD HOUR EXAM
covering everything in the complex variable area including
those parts of Chapters 12 through 16 discussed in class. The
exam will be closed book but you can bring one 3x5"card and
your calculator. 
![]()
