| EGM 3520-MECHANICS OF MATERIALS
SUMMER TERM 2002 |

| EGM 3520-MECHANICS OF MATERIALS
SUMMER TERM 2002 |
This summer I will be teaching the STRENGTH OF MATERIALS class EGM 3520. We meet MWF 4th period in Aero 303 (12:30 till 1:45pm). The book we are using is MECHANICS OF MATERIALS 4th Edition by H.C.Hibbeler. You can reach me at anytime via e-mail at kurzweg@ufl.edu . Your TAs this summer will be Carmen Savu( csavu@ufl.edu ) and Jongyoon Ok ( jongyoon@grove.ufl.edu ). They will grade your homeworks, make up pdf files for the solutions, grade your three tests, plus be available for tutoring in NEB107. Tutoring hours for Mr.Ok will be T,R,F 4-5pm, those for Ms.Savu are M,T,W 2:30-4pm . Make use of them. The knight on horeseback points to the next lexture.
Do you recognize the individuals in the above pictures? They are from left to right Leonardo da Vinci(1452-1519), Isaac Newton(1642-1727) and Galileo Galilei(1564-1642).
CEIINOSSITTUV-Robert Hooke's(1635-1703) famous anagram to protect his priority to Hooke's law , which in Latin states UT TENSIO, SIC VIS and which on translation into English(using my two years of high school Latin) reads AS THE EXTENTION, SO THE FORCE. Hooke and Newton were contemporaries and they apparently couldn't stand each other and each claimed the other was stealing his ideas. There is no picture extant today of Hooke because Newton (as president of the Royal Society after Hooke's death), saw to it that all of Hooke's equipment and scientific and other papers (which were stored at the Society) were lost.

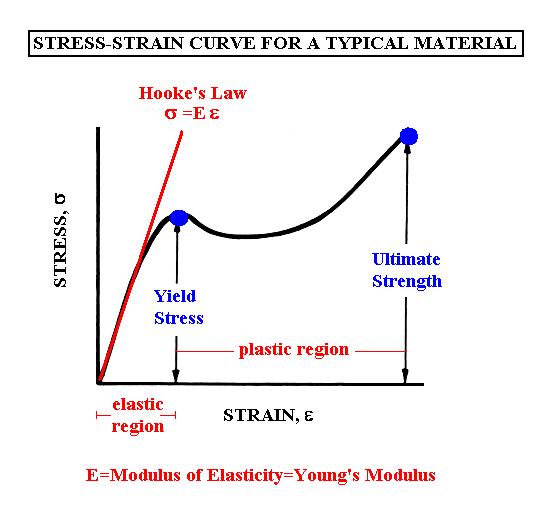
Friday May 17th-Stress-Strain Curves,
Ductile
and Brittle Materials, Loading and Unloading, Fatique. The general
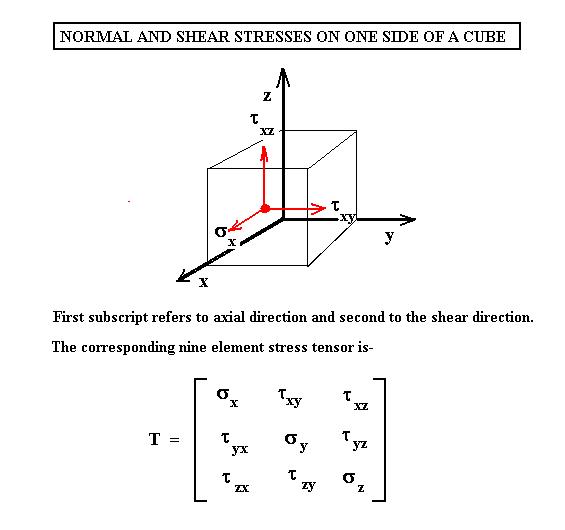
Stress
Tensor T. Poisson Ratio.
Statically Indeterminate Problems. Thermal Strain and Forces created by Thermal Expansion.
Poisson's Ratio. Generalized Hooke's Law. Dilation of a Cube subjected to Axial Stresses. Shear Modulus.
More on Shearing Strain. Bulk Modulus. Saint-Venant's Principle. Stress Concentrators and Plastic Deformations.
IMPORTANT QUANTITES: We are now sufficiently far into the course to list the more important quantities arising in the strength of materials. Here they are:
(1) Normal Stress = s = Axial Load/ Cross-Sectional Area
(2) Shear Stress = t = Shear Force/ Area Tangent to Force
(3) Strain = e = Change in Length/ Length
(4) Young's Modulus( or Modulus of Elasticity) = E, where by Hooke's Law s=E e
(5) Poisson's Ratio = n = -(Transverse Strain/ Axial Strain). Range of values of n is 0<n<0.5
(6) Dilation = e = Change in Volume/Volume = Sum of Strains in the x, y and z directions
(7) Modulus of Rigidity = Shear Modulus = G = Shearing Stress/ Shearing Strain
(8) Bulk Modulus= k = E/[3(1-2n )]. Note k becomes infinite as the incompressible limit of n=0.5 is reached.
We will add to this list in coming lectures.
May 27- Introduction to Torsion in Rods and Pipes. Derivation of the Elastic Torsion Formula. Maximum Shear Stress.
ELASTIC FORMULA FOR TORSION: Consider a shaft of radius R and length L . Let its left end be anchored to a rigid plate and the right end twisted about its axis by an angle phi due to an applied torque T. From the geometry one sees that the shear strain(gamma) relates to the twist angle(phi) by the small angle approximation (gamma) x (L) = (phi) x (r) , at radial distance 0<r<R from the shaft axis. Also within the elastic range we have from Hooke's Law that the shear stress tau = G x (gamma). Next, from calculus we have that T=Integral[r x (tau) x dA]= (phi) x (G/L) Integral[r x r x dA]. Recognizing that this last integral is just the polar area moment of inertia J and that the maximum shear at the shaft surface is taumax=(R/r) x (tau), one arrives at the elastic formula for torsion taumax=RT/J. From this formula one can calculate the largest torque which may be applied to a shaft(or pipe by the superposition principle) yet keep the maximum shear stress below the yield point of the material in question. An interesting result predicted by this formula is that( for the same cross-sectional area of material) a hollow shaft can handle larger torques than one which is solid.
May 29- More on Torsion. Angle of Twist and its use in determining the Shear Modulus G. The Cavendish torsion fibre experiment for determining the universal gravitational constant. Maximum Power Transmitted along a Rotating Shaft without exceeding the Maximum Allowable Shear. Your FIRST HOUR EXAM is scheduled for Monday June 8th. It will cover the first three chapters in the book and will be a one hour in-class exam. You can bring one 3"x 5" card but otherwise it's closed book.
ANGLE OF TWIST : We have shown last time that a shaft subjected to a torque of T about its axis will produce a twist in the shaft when the other end is held fixed. The value of this twist angle follows directly from the geometry which shows that (gamma) x L= (phi) x R , where gamma is the shear strain maximum, L the shaft length , R the shaft radius and phi the twist angle. Solving this for phi , after recalling that taumax=TR/J=G x (gamma), one has that phi= TL/JG. Although this angle is typically very small it can become appreciable for very long rods of small diameter. Take , for example, a steel pipe of 3" outer radius , 2.5 " inner radius, and of 2 mile length used in oil drilling. For this pipe J=37.398 in^4 and G=11.2 million psi. If the applied driving torque is 1400 ft-lb, one finds a twist angle of phi= 5.08 radians= 291.2 degrees. The maximum shear stress produced under this condition is taumax=1.347 ksi. This is only a small fraction of the yield strength in shear of about 20 ksi for steel. Thus things will remain elastic.
June 1-Additional information on torsion. Twist of a shaft with variable properties along its length. Stress concentration at fillets. Torsion for non-circular members and for thin walled shafts. Plastic deformations in shafts.
June 5- Review of the first three chapters in preparation for Monday's exam.
June 8-First Hour Exam.
June 10-Introduction to Bending. Derivation of the Elastic Flexure Formula relating axial stress to distance from the neutral axis. Curvature of the Neutral Surface produced by a Moment.
BASIC EQUATIONS FOR BENDING OF A BEAM: Consider a horizontal beam of length L which is supported at its ends and is slightly bent by an external transverse loading or by its own weight. Let the radius of curvature of the bending(measured from the neutral axis) be R, so that the angle of the sector formed is just L/R. The assumed rectangular cross-sectional area is taken as A =wh and the beam height is h and the width w. At the top of the beam one has a compression while at the bottom there is a tension due to the bending. The axial strain varies with perpendicular distance y from the beams neutral axis and , within the elastic limit, corresponds to an axial normal stress of sigmax=-E y /R, where E is the Young's modulus. Since the net axial force must be zero, one sees at once that the neutral axis coincides with the centroidal axis of the cross-section. The total internal moment about the z axis , at a fixed axial position x , is Mz= (E/R)integral[ y2 dA]=IE/R , where I is the area moment of inertia about the z axis passing at right angles through the neutral axis. We can also eliminate R from the above two equations to get the elastic flexure formula max[sigma x]=Mzc/I , where c=h/2 is the beam half-height. The quantity S=I/c is referred to as the elastic section modulus and one wants to have this modulus large when the moment acting is large in order to not exceed the maximum allowable axial stress occuring at the top(max compression)and the bottom( max tension)of the beam. We also see from the second of the above equations that small bending(and hence large radius of curvature R) occurs for large I = wh3/12. That is the reason floor and ceiling joists intended to carry heavy loads generally have h>>w.
June 12-Bending of I beams and other cross-section beams. Bending of beams made of several different materials. Reinforced concrete beams.
June15- Reinforced Concrete Beams. Stress Concentrators. Eccentric Loading and yield on Link of Chain. Plastic Loading and Residual Stress.
RESULTS OF FIRST EXAM: I just got back the results of your first exam. Out of a possible maximum score of 30 points, the class had an average of 26.4 points and there were 23 perfect papers. Good show! The next exam will be a little more difficult , but there should be no problem for those of you keeping up with the class work and your homework.
ANOTHER DIVERSION: Interested in the latest Science and Technology News? If so, you can go to one of the following:
June 17-Completion of the Chapter on Bending. Bending of Composite Beams. Unsymmetric Bending. Bending of Curved Members.
June 19-Introduction to Transverse Loading. Shear Flow Formula. Shearing Stresses in Beams.
AXIAL SHEAR STRESS IN A CANTILEVER BEAM- Consider a cantilever beam of negligible weight and rectangular cross-section 2c*w subjected to a vertical point force F at its free end. This force produces a vertical shear V=-F and a bending moment M=Fx in the beam at distance x from the free end. We already know from earlier discussions that the axial normal stress in the beam is sigma =My/I. This becomes sigma=Vxy/I for the present set-up. Since sigma varies with both y and x, we expect an axial shear to exist in the beam. The shear force at x along the plane defined by y=y will be H=integral[sigma*dA]=[xV/I]*integral[y*dy*w]. But this last integral represents the first moment of area (c-y)*w with respect to the neutral axis. It is denoted by Q, and equals the product of (c-y)*w and ybar , the last being the distance from the neutral axis to the centroid of this cross-sectional area. One defines the shear flow q as q=H/x=VQ/I , so that the axial shear stress at x becomes tau=q*dx/(dx*w)=VQ/I*w). Note that this shear stress vanishes at the beam top and bottom surfaces at y=c and y=-c, since Q is zero there. Inside the beam, however, the axial shear stress has a parabolic dependence and reaches a maximum of tau=3V/2A along the neutral surface.
June 29, 1998-After a week of mid-summer semester break, we are back to continue our discussions in the Strength of Materials. Today we say more about internal shearing stresses in beams. In particular, we talk about such stresses in T and Box beams and discuss the shear exerted at a glue surface holding together two components of a composite beam. Also something on plasticity of beams.
July 1-Completion of Chapter on Shear. Stresses for Thin walled Members. Stresses under Combined Loadings. No classes Friday July 3 because of July 4th. The Second Hour Exam is scheduled for Wednesday July 8 and will concentrate on Chapters 4(Bending) and 5(Shear). Format will be the same as for the first exam. There will be three out of four questions to answer.
ANOTHER DIVERSION-Last week a new service became available on the Internet. It gives satellite and aerial photos obtained by the US and Russia for most of the United States and also a good part of Western Europe. You can access this free service at:
To give you some idea of what these photos( which do not have the resolution of classified military info capable of guiding cruise missiles to their intended target) can reveal, I show you an image *of the Aero Building in which we hold our classes . (*-thanks to Damon Clark, our webmaster, for putting together the four picture mosaic I had originally into a single image)

July 6-Review for the Second Hour Exam.
July 8,1998- Second Hour Exam.
July 10-Transformation Equation for Plane Stress. Derivation of the Mohr Circle.
A STRENGTH OF MATERIALS COURSE ON THE NET: I have just run across a Strength of Materials course offered on the WEB by the University of Wisconsin-Stout in Menomonie. It summarizes very nicely various topics in Strength and does so without the excessive verbiage of most texts. You may want to consult it once in a while as a supplement to the book and the lectures. It is found at-
RESULTS OF SECOND EXAM: Your second exam has been graded and will be handed back at our next meeting. This time the class average was 23.5 points out of a maximum possible of 30 points. There was one perfect paper. There is one more exam scheduled for Friday July 31, 1998.
July 15-Completion of Chapter VI. Stresses in Thin-Walled Vessels. Mohr Circle for Plane Strain.
July 17-Shear and Bending Moments in Prismatic Beams. Derivation of dV(x)/dx=-w(x) and of dM(x)/dx=V(x) Equations.
July 20-Design of prismatic beams so as to not exceed the maximum allowable axial normal and shearing stresses for a given loading condition. Beams of variable cross-section having constant strength.
July 22-Deflection of Beams by Integration. Derivation of the Elastic Curve Formula y"=M(x)/EI and maximum deflection for cantilever and uniformely loaded beam.
July 24-Some more on the Deflection of Beams including the Superposition concept. Introduction to the Stability of Columns and Euler's Buckling Formula. Also the Student Assesment Forms to be filled out. Last assignment is to Read pgs. 478-530, 631-688, and to do problems 8.12, 8.430, 8.60,11.2,11.22. This assignment will not be collected or graded, but it will nevertheless be a good idea for you to work it out prior to the Third Exam to be given next Friday.
July 27-More on Euler Buckling of Columns for Different End Conditions. This will be the last lecture on new material in the course.
July 29-Review for Third Exam covering Chapters VI(Stress-Strain Transformations),VII(Design of Prismatic Beams for Strength),VIII(Deflection of Beams by Integration), and IX(Stability of Elastic Columns).
DIVERSION ON ENCRYPTION USING IRRATIONAL NUMBERS : I have always been fascinated with irrational numbers, that is, numbers which cannot be expressed as the ratio of two integers and exibit no repetitive patterns when written out in decimal form. There are an infinite number of such numbers , the best known of which are pi, e and sqrt(2). With the advent of high speed electronic computers over the last half century, some of these numbers(especially pi) have now been evaluated to well over a billion places. Although these numbers do not exibit a periodic structure, the value of the integer at the nth position for a given irrational number is unique. Thus pi at the twentieth place to the right of the decimal point shows the integer six. This can be written in shorthand as pi(20)=6. Likewise e(7)=8, and sqrt2(13)=0. One could encrypt a message using a combination of several irrational numbers as a one key in conjunction with a second key known only to the sender and receiver. Constructing a table of the sequential integers of pi with 26 (or an integer multiple of 26) integers per line representing the alphabet, one could then construct an encoded message using as the second key something like GO GATORS, to describe the rows in the table . The resultant message would then reduce to just a sequence of integers from 0 through 9, and since there are only ten integers but 26 letters involved, the coding and decoding will introduce an ambiquity which will make the code essentially impossible to crack by an outsider not knowing the infinite number of possible key combinations being used ( for example , the first key could be given by sqrt(e)*pi^3), no matter how many computer runs are made. Try writing a message using such an encrytion approach. To help you, here is pi written out to 949 places. Click on LINK1 and LINK2 to get the information. If you want to learn more about cryptography, including the stuff on the enigma machine of WWII, then read the interesting paperback The Code Breakers by D.Kahn. A major resurgence in encrytion interest has been brought about in the last few years because of the need to be able to make secure financial transactions and send secure e-mail via the internet. In this last regard you might want to look at the PGP dual key code available via ftp. It is discussed in detail in the book Protect Your Privacy by W. Stallings. PGP stands for pretty good privacy and uses both a private and public key, one of which has a huge random number length corresponding to 1024=2^10 bits. PGP is considered unbreakable with today's computer capabilities.
July 31-THIRD HOUR EXAM. Same format as earlier two exams with 3 out of 4 questions to answer. It's closed book but you can bring one 3"x 5" card. Things will be graded by Monday morning August 3rd and I should have your course grades ready by later that afternoon. As first announced at the beginning of the course, your grade is determined by the formula-
LAST DIVERSION: Interested in foreign languages? The Alta Vista search engine furnishes a free translation service which will give you a rough idea of what is being said in a foreign language and also allows translation from English into that language. To do so, go to-
I'll give you an example. Lets translate the following statement(which happens to be my own view):http://babelfish.altavista.com/
"The most successful people in life are those who choose a path along which their interest and talent lies"
In Spanish-
"La
gente más acertada de la vida es las que eligen una trayectoria
a lo largo de
la cual su interés y talento mienta"
In German-
"Die erfolgreichsten Leute im Leben sind die, die einen Weg
wählen,
entlang
dem ihr Interesse und Talent liegt"
In French-
"Les personnes les plus réussies dans la vie sont ceux qui
choisissent
un chemin
le long dont leur intérêt et talent se trouve"
As those of you familiar with these languages will note, the machine translation is not the best but it does get the central idea across.
August 1, 1998-I have graded your third exam(mean out of 30 points was 24.5 and there were 7 perfect papers)and will base your final course grades (ready by Monday)on the folowing scale: 89.4<A<100, 88=B+, 79<B<88, 78=C+, 66<C<78, 62<D+<65, 54<D<62.
Some Related Links: