Surrogate-based design optimization
|
|
|
(a) Actual response.
|
(b) Kriging model with 12 observations
|
Figure 1: Surrogate modeling in action.
A surrogate-based design optimization (SBDO) cycle
consists of choosing points in design space (design of experiments),
conducting simulations at these points and fitting surrogates to expensive
responses. If the fitted surrogate satisfies measures of accuracy, we use
it to conduct design optimization and then verify the optimum we obtain by
exact simulation. Then, if it appears that further improvements in the
design can be made by improving the surrogate, we zoom on regions of
interest and conduct another cycle. This process is illustrated by Figure 2.
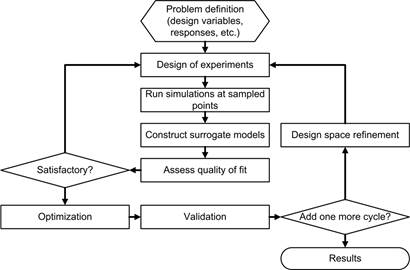
Figure 2: Surrogate based design optimization.
In surrogate-based design optimization, the research of
the Structural and Multidisciplinary Optimization Group involves:
·
Uncertainty quantification: besides
prediction, surrogates also provide uncertainty estimates. These estimates
are used to select points to be sampled in the next optimization cycle and
also to stop the optimization task. Our research focus on (i) using the information given by multiple surrogates
to improve or provide uncertainty estimates; and (ii) using the uncertainty
estimates to improve the robustness of the optimization results.
·
Uncertainty minimization: an appropriate
choice of the design of experiments allows to minimize the uncertainty (and
the error) of the surrogate. Our research focus on (i)
adapted design of experiments for constrained optimization (when a
surrogate is used to approximate a constraint function), and (ii) efficient
allocation of resources for reliability based optimization.
·
Assessing the value of another cycle in surrogate-based
optimization. Our research focus on providing accurate estimates of the
probability of achieving a target level of improvement in the next cycle.
·
Cross-validation and bootstrap: with limited
data and computational resources, the available data must also be used to
access the quality of the information given by the fitted surrogate. Our
research focus on (i) cross-validation and
bootstrap for design of conservative surrogates (metamodels
that safely predicts the actual response); (ii) cross-validation for
ranking the quality of prediction and correlation of uncertainty estimates.
|